In the previous section devoted to the plane in space, we examined the issue from the perspective of geometry. Now let's move on to describing the plane using equations. A look at the plane from the side of algebra involves considering the main types of plane equations in rectangular system coordinates O x y z three-dimensional space.

Yandex.RTB R-A-339285-1

Definition of the equation of a plane

Definition 1

Plane- This geometric figure, consisting of individual points. Each point in three-dimensional space corresponds to coordinates that are specified by three numbers. The plane equation establishes the relationship between the coordinates of all points.

The equation of the plane in the rectangular coordinate system 0xz has the form of an equation with three variables x, y and z. The coordinates of any point lying within the given plane satisfy the equation; the coordinates of any other points that lie outside the given plane do not satisfy.

Substituting a point in a given plane into the equation of a coordinate plane turns the equation into an identity. When substituting the coordinates of a point lying outside the plane, the equation turns into an incorrect equality.

The plane equation can have several types. Depending on the specifics of the problems being solved, the plane equation can be written in different ways.

General plane equation

Let's formulate the theorem and then write down the equation of the plane.

Theorem 1

Any plane in a rectangular coordinate system O x y z in three-dimensional space can be specified by an equation of the form A x + B y + C z + D = 0, where A, B, C and D– some real numbers that are not equal to zero at the same time. Any equation of the form A x + B y + C z + D = 0 defines a plane in three-dimensional space

An equation of the form A x + B y + C z + D = 0 is called general equation plane. If you don't attach numbers A, B, C And D specific values, then we obtain the equation of the plane in general form.

It is important to understand that the equation λ · A x + λ · B y + λ · C z + λ · D = 0 will define the plane in exactly the same way. In the equation, λ is some non-zero real number. This means that the equalities A x + B y + C z + D = 0 and λ · A x + λ · B y + λ · C z + λ · D = 0 are equivalent.

Example 1

The general equations of the plane x - 2 · y + 3 · z - 7 = 0 and - 2 · x + 4 · y - 2 3 · z + 14 = 0 are satisfied by the coordinates of the same points located in three-dimensional space. This means that they define the same plane.

Let us give an explanation of the theorem discussed above. A plane and its equation are inseparable, since each equation A x + B y + C z + D = 0 corresponds to a plane in a given rectangular coordinate system, and each plane located in three-dimensional space corresponds to its equation of the form A x + B y + C z + D = 0.

The plane equation A x + B y + C z + D = 0 can be complete or incomplete. All coefficients A, B, C and D in the complete equation are different from zero. Otherwise, the general equation of the plane is considered incomplete.

Planes that are specified by incomplete equations can be parallel to the coordinate axes, pass through the coordinate axes, coincide with or parallel to the coordinate planes, and pass through the origin of coordinates.

Example 2

Consider the position in space of the plane given by the equation 4 · y - 5 · z + 1 = 0.

It is parallel to the x-axis and located perpendicular to the O y z plane. The equation z = 0 defines the coordinate plane O y z, and the general equation of the plane of the form 3 x - y + 2 z = 0 corresponds to the plane that passes through the origin.

Important clarification: coefficients A, B and C in the general equation of the plane represent the coordinates of the normal vector of the plane.

When they talk about the equation of a plane, they mean the general equation of a plane. All types of plane equations, which we will discuss in the next section of the article, are obtained from the general plane equation.

Normal plane equation

A normal plane equation is a general plane equation of the form A x + B y + C z + D = 0, which satisfies the following conditions: the length of the vector n → = (A, B, C) is equal to one, i.e. n → = A 2 + B 2 + C 2 = 1, and D ≤ 0.

Also, writing the normal equation of a plane can have the following form cos α · x + cos β · y + cos γ · z - p = 0, where p is a non-negative number that is equal to the distance from the origin to the plane, and cos α, cos β, cos γ are the direction cosines of the normal vector of a given plane of unit length.

n → = (cos α , cos β , cos γ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

That is, according to the normal equation of the plane, the plane in the rectangular coordinate system O x y z is removed from the origin by a distance p in the positive direction of the normal vector of this plane n → = (cos α, cos β, cos γ). If p equals zero, then the plane passes through the origin.

Example 3

The plane is given by the general plane equation of the form - 1 4 · x - 3 4 · y + 6 4 · z - 7 = 0. D = - 7 ≤ 0, the normal vector of this plane n → = - 1 4, - 3 4, 6 4 has a length equal to one, since n → = - 1 4 2 + - 3 4 2 + 6 4 = 1. Accordingly, this general plane equation is a normal plane equation.

For a more detailed study of the normal plane equation, we recommend going to the appropriate section. The topic provides analysis of problems and typical examples, as well as methods for bringing the general equation of a plane to normal form.

The plane cuts off segments of a certain length on the coordinate axes O x, O y and O z. The lengths of the segments are specified by non-zero real numbers a, b and c. The plane equation in segments has the form x a + y b + z c = 1. The sign of the numbers a, b and c shows in which direction from the zero value the segments on the coordinate axes should be plotted.

Example 4

Let us construct a plane in a rectangular coordinate system, which is specified by the equation of the plane formula in the segments x - 5 + y - 4 + z 4 = 1.

The points are removed from the origin in the negative direction by 5 units along the abscissa axis, by 4 units in the negative direction along the ordinate axis, and by 4 units in the positive direction along the applicate axis. Mark the points and connect them with straight lines.

The plane of the resulting triangle is the plane corresponding to the equation of the plane in segments, having the form x - 5 + y - 4 + z 4 = 1.

More detailed information about the equation of a plane in segments and bringing the equation of a plane in segments to the general equation of a plane is available in a separate article. There are also a number of solutions to problems and examples on the topic.

If you notice an error in the text, please highlight it and press Ctrl+Enter

Equation of a plane, types of equation of a plane.

In the section plane in space, we examined the plane from a geometry perspective. In this article we will look at the plane from the perspective of algebra, that is, we will move on to describing the plane using the equation of the plane.

First, let's look at the question: “What is the equation of a plane”? After this, we will consider the main types of plane equations in a rectangular coordinate system Oxyz three-dimensional plane.

Page navigation.

Equation of a plane - definition.
General equation of the plane.
Equation of a plane in segments.
Normal plane equation.

Equation of a plane - definition.

Let a rectangular coordinate system be fixed in three-dimensional space Oxyz and a given plane.

A plane, like any other geometric figure, consists of points. In a rectangular coordinate system Oxyz Each point corresponds to an ordered triple of numbers - the coordinates of the point. A relationship can be established between the coordinates of each point on the plane using an equation called the plane equation.

Plane equation in a rectangular coordinate system Oxyz in three-dimensional space is an equation with three variables x, y And z, which is satisfied by the coordinates of any point in a given plane and not satisfied coordinates of points, lying outside this plane.

Thus, the equation of the plane becomes an identity when the coordinates of any point of the plane are substituted into it. If you substitute the coordinates of a point that does not lie in this plane into the equation of a plane, it will turn into an incorrect equality.

It remains to find out what form the equation of the plane has. The answer to this question is contained in the next paragraph of this article. Looking ahead, we note that the plane equation can be written in different ways. Existence various types equations of the plane are determined by the specifics of the problems being solved.

Top of page

General equation of the plane.

Let us present the formulation of the theorem, which gives us the form of the plane equation.

Theorem.

Any equation of the form , where A, B, C And D– some real numbers, and A, IN And C are not equal to zero at the same time, defines a plane in a rectangular coordinate system Oxyz in three-dimensional space, and every plane in a rectangular coordinate system Oxyz in three-dimensional space can be given by an equation of the form .

The equation is called general plane equation in space. If you don't attach numbers A, IN, WITH And D specific values, then the general equation of the plane is called plane equation in general form.

It should be noted that an equation of the form , where is some real number other than zero, will define the same plane, since the equalities and are equivalent. For example, the general equations of the plane and specify the same plane, since they are satisfied by the coordinates of the same points in three-dimensional space.

Let us explain a little the meaning of the stated theorem. In a rectangular coordinate system Oxyz each plane has its corresponding equation general view, and each equation corresponds to a plane in a given rectangular coordinate system of three-dimensional space. In other words, the plane and its general equation are inseparable.

If all coefficients A, IN, WITH And D in the general equation the planes are non-zero, then it is called complete. Otherwise, the general equation of the plane is called incomplete.

Incomplete equations specify planes parallel to coordinate axes, passing through coordinate axes, parallel to coordinate planes, perpendicular to coordinate planes, coinciding with coordinate planes, as well as planes passing through the origin of coordinates.

For example, plane parallel to the x-axis and perpendicular to the coordinate plane Oyz, the equation z = 0 defines the coordinate plane Oxy, and the general plane equation is of the form corresponds to the plane passing through the origin.

Note also that the coefficients A, B And C in the general equation, the planes represent the coordinates of the normal vector of the plane.

All equations of the plane, which are discussed in the following paragraphs, can be obtained from the general equation of the plane, and also reduced to the general equation of the plane. Thus, when they talk about the equation of a plane, they mean the general equation of a plane, unless otherwise stated.

Top of page

Equation of a plane in segments.

View plane equation , where a, b and c are non-zero real numbers, is called equation of the plane in segments.

This name is not accidental. Absolute values numbers a, b and c are equal to the lengths of the segments that the plane cuts off on the coordinate axes Ox, Oy and Oz, respectively, counting from the origin. The sign of the numbers a, b and c indicates in which direction (positive or negative) the segments should be plotted on the coordinate axes.

For example, let’s construct a plane in the rectangular coordinate system Oxyz, defined by the equation of the plane in segments . To do this, mark a point that is 5 units away from the origin in the negative direction of the abscissa axis, 4 units in the negative direction of the ordinate axis, and 4 units in the positive direction of the applicate axis. All that remains is to connect these points with straight lines. The plane of the resulting triangle is the plane corresponding to the equation of the plane in segments of the form .

To get more complete information refer to the article equation of a plane in segments, it shows the reduction of the equation of a plane in segments to the general equation of a plane, there you will also find detailed solutions typical examples and tasks.

Normal plane equation.

The general equation of a plane of the form is called normal plane equation, If equal to one, that is, , And .

You can often see that the normal equation of a plane is written as . Here are the direction cosines of the normal vector of a given plane of unit length, that is, and p is a non-negative number equal to the distance from the origin to the plane.

The normal equation of a plane in the rectangular coordinate system Oxyz defines a plane that is removed from the origin by a distance p in the positive direction of the normal vector of this plane . If p=0, then the plane passes through the origin.

Let us give an example of a normal plane equation.

Let the plane be specified in the rectangular coordinate system Oxyz by the general equation of the plane of the form . This general equation of the plane is the normal equation of the plane. Indeed, the normal vector of this plane is has a length equal to one, since .

The plane equation in normal form allows you to find the distance from a point to a plane.

We recommend that you understand this type of plane equation in more detail, look at detailed solutions to typical examples and problems, and also learn how to reduce the general plane equation to normal form. You can do this by referring to the article.

Bibliography.

Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Kiseleva L.S., Poznyak E.G. Geometry. Textbook for 10-11 grades of secondary school.
Bugrov Ya.S., Nikolsky S.M. Higher mathematics. Volume one: elements of linear algebra and analytical geometry.
Ilyin V.A., Poznyak E.G. Analytic geometry.

Equation of a plane. How to write an equation of a plane?
Mutual arrangement of planes. Tasks

Spatial geometry is not much more complicated than “flat” geometry, and our flights in space begin with this article. To master the topic, you need to have a good understanding of vectors, in addition, it is advisable to be familiar with the geometry of the plane - there will be many similarities, many analogies, so the information will be digested much better. In a series of my lessons, the 2D world opens with an article Equation of a straight line on a plane. But now Batman has left the flat TV screen and is launching from the Baikonur Cosmodrome.

Let's start with drawings and symbols. Schematically, the plane can be drawn in the form of a parallelogram, which creates the impression of space:

The plane is infinite, but we have the opportunity to depict only a piece of it. In practice, in addition to the parallelogram, an oval or even a cloud is also drawn. For technical reasons, it is more convenient for me to depict the plane in exactly this way and in exactly this position. Real planes, which we will consider in practical examples, can be located in any way - mentally take the drawing in your hands and rotate it in space, giving the plane any slope, any angle.

Designations: planes are usually denoted in small Greek letters, apparently so as not to confuse them with straight line on a plane or with straight line in space. I'm used to using the letter . In the drawing it is the letter “sigma”, and not a hole at all. Although, the holey plane is certainly quite funny.

In some cases, it is convenient to use the same Greek letters with lower subscripts to designate planes, for example, .

It is obvious that the plane is uniquely defined by three different points that do not lie on the same line. Therefore, three-letter designations of planes are quite popular - by the points belonging to them, for example, etc. Often letters are enclosed in parentheses: , so as not to confuse the plane with another geometric figure.

For experienced readers I will give quick access menu:

How to create an equation of a plane using a point and two vectors?
How to create an equation of a plane using a point and a normal vector?

and we will not languish in long waits:

General plane equation

The general equation of the plane has the form , where the coefficients are not equal to zero at the same time.

A number of theoretical calculations and practical problems are valid both for the usual orthonormal basis and for the affine basis of space (if the oil is oil, return to the lesson Linear (non) dependence of vectors. Basis of vectors). For simplicity, we will assume that all events occur in orthonormal basis and Cartesian rectangular coordinate system.

Now let’s practice our spatial imagination a little. It’s okay if yours is bad, now we’ll develop it a little. Even playing on nerves requires training.

In the very general case, when the numbers are not zero, the plane intersects all three coordinate axes. For example, like this:

I repeat once again that the plane continues indefinitely in all directions, and we have the opportunity to depict only part of it.

Let's consider the simplest equations of planes:

How to understand given equation? Think about it: “Z” is ALWAYS equal to zero, for any values of “X” and “Y”. This is the equation of the "native" coordinate plane. Indeed, formally the equation can be rewritten as follows: , from where you can clearly see that we don’t care what values “x” and “y” take, it is important that “z” is equal to zero.

Likewise:
– equation of the coordinate plane;
– equation of the coordinate plane.

Let's complicate the problem a little, consider a plane (here and further in the paragraph we assume that the numerical coefficients are not equal to zero). Let's rewrite the equation in the form: . How to understand it? “X” is ALWAYS, for any values of “y” and “z”, equal to a certain number. This plane is parallel to the coordinate plane. For example, a plane is parallel to a plane and passes through a point.

Likewise:
– equation of a plane that is parallel to the coordinate plane;
– equation of a plane that is parallel to the coordinate plane.

Let's add members: . The equation can be rewritten as follows: , that is, “zet” can be anything. What does it mean? “X” and “Y” are connected by the relation, which draws a certain straight line in the plane (you will find out equation of a line in a plane?). Since “z” can be anything, this straight line is “replicated” at any height. Thus, the equation defines a plane parallel to the coordinate axis

Likewise:
– equation of a plane that is parallel to the coordinate axis;
– equation of a plane that is parallel to the coordinate axis.

If the free terms are zero, then the planes will directly pass through the corresponding axes. For example, the classic “direct proportionality”: . Draw a straight line in the plane and mentally multiply it up and down (since “Z” is any). Conclusion: the plane defined by the equation passes through the coordinate axis.

We complete the review: the equation of the plane passes through the origin. Well, here it is quite obvious that the point satisfies this equation.

And finally, the case shown in the drawing: – the plane is friendly with all coordinate axes, while it always “cuts off” a triangle, which can be located in any of the eight octants.

Linear inequalities in space

To understand the information you need to study well linear inequalities in the plane, because many things will be similar. The paragraph will be of a brief overview nature with several examples, since the material is quite rare in practice.

If the equation defines a plane, then the inequalities
ask half-spaces. If the inequality is not strict (the last two in the list), then the solution of the inequality, in addition to the half-space, also includes the plane itself.

Example 5

Find the unit normal vector of the plane .

Solution: A unit vector is a vector whose length is one. Let us denote this vector by . It is absolutely clear that the vectors are collinear:

First, we remove the normal vector from the equation of the plane: .

How to find a unit vector? In order to find the unit vector, you need every divide the vector coordinate by the vector length.

Let's rewrite the normal vector in the form and find its length:

According to the above:

Answer:

Verification: what was required to be verified.

Readers who carefully studied the last paragraph of the lesson probably noticed that the coordinates of the unit vector are exactly the direction cosines of the vector:

Let's take a break from the problem at hand: when you are given an arbitrary non-zero vector, and according to the condition it is required to find its direction cosines (see the last problems of the lesson Dot product of vectors), then you, in fact, find a unit vector collinear to this one. Actually two tasks in one bottle.

The need to find the unit normal vector arises in some problems of mathematical analysis.

We’ve figured out how to fish out a normal vector, now let’s answer the opposite question:

How to create an equation of a plane using a point and a normal vector?

This rigid construction of a normal vector and a point is well known to the dartboard. Please stretch your hand forward and mentally select an arbitrary point in space, for example, a small cat in the sideboard. Obviously, through this point you can draw a single plane perpendicular to your hand.

The equation of a plane passing through a point perpendicular to the vector is expressed by the formula:

12.1. Basic Concepts

Surface and its equation

A surface in space can be considered as a locus of points that satisfy some condition. For example, a sphere of radius R with a center at point O 1 is the geometric locus of all points in space located at a distance R from point O 1.

The rectangular coordinate system Oxyz in space allows us to establish a one-to-one correspondence between points in space and triples of numbers x, y and z - their coordinates. A property common to all points on a surface can be written as an equation connecting the coordinates of all points on the surface.

The equation of a given surface in the rectangular coordinate system Oxyz is the equation F(x, y, z) = 0 with three variables x, y and z, which is satisfied by the coordinates of each point lying on the surface, and not satisfied by the coordinates of points not lying on this surface surfaces. The x, y, and z variables in the surface equation are called the current coordinates of the surface points.

The surface equation allows the study of the geometric properties of a surface to be replaced by the study of its equation. So, in order to find out whether a point M 1 (x 1 ;y 1 ;z 1) lies on a given surface, it is enough to substitute the coordinates of the point M 1 into the equation of the surface instead of variables: if these coordinates satisfy the equation, then the point lies on surfaces, if they do not satisfy, they do not lie.

Sphere equation

Let's find the equation of a sphere of radius R with center at point O 1 (x 0 ;y 0 ;z 0).

According to the definition of a sphere, the distance of any of its points M(x; y; z) from the center O 1 (x 0 ;y 0 ;z 0) is equal to the radius R, i.e. O 1 M= R. But, where . Hence,

This is the required equation of the sphere. It is satisfied by the coordinates of any of its points and is not satisfied by the coordinates of points that do not lie on the given sphere.

If the center of the sphere Ο 1 coincides with the origin of coordinates, then the equation of the sphere takes the form .

If an equation of the form F(x;y;z) = 0 is given, then, generally speaking, it defines a certain surface in space. The expression "generally speaking" means that in in some cases

the equation F(x; y; z) = 0 may not define a surface, but a point, a line, or not define any geometric image at all. They say “the surface degenerates.”

Thus, the equation is not satisfied by any real values of x, y, z. The equation is satisfied only by the coordinates of points lying on the Ox axis (from the equation it follows: y = 0, z = 0, and x is any number).

So, a surface in space can be defined geometrically and analytically.

This leads to the formulation of two main tasks:

1. A surface is given as a locus of points. Find the equation of this surface.

2. Given the equation F(x;y;z) = 0. Investigate the shape of the surface defined by this equation.

Equations of a line in space A line in space can be considered as the line of intersection of two surfaces (see Fig. 66) or as the locus of points common to two surfaces. If

(12.1)

Comparisons of system (12.1) are called equations of a line in space.

For example, there are equations for the Ox axis.

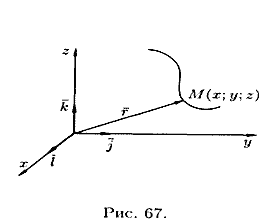
A line in space can be considered as the trajectory of a point (see Fig. 67). In this case, it is given by the vector equation

or parametric equations

projections of vector (12.2) on the coordinate axes.

For example, the parametric equations of a helix have the form

If point M moves uniformly along the generatrix of a circular cylinder, and the cylinder itself rotates uniformly around the axis, then point M describes a helical line (see Fig. 68).

12.2. Equations of a plane in space The simplest surface is a plane. The plane in Oxyz space can be specified different ways

. Each of them corresponds to a certain type of its equation.

Equation of a plane passing through a given point perpendicular to a given vector Let the plane Q in Oxyz space be defined by a point and vector perpendicular to this plane (see Fig. 69). Let us derive the equation of the plane Q. Take an arbitrary point on it and compose a vector. For any location of the point M on the plane Q, the vectors and are mutually perpendicular, therefore they scalar product

(12.3)

equals zero: , i.e.

The coordinates of any point on the Q plane satisfy equation (12.3); the coordinates of points not lying on the Q plane do not satisfy this equation (for them ). Equation (12.3) is called the equation of the plane passing through a given point

perpendicular to the vector. It is of the first degree relative to the current coordinates x, y, z. The vector is called the normal vector of the plane. Giving coefficients A, B and C to equation (12.3) different meanings

General plane equation

, you can get the equation of any plane passing through the point . The set of planes passing through a given point is called a bundle of planes, and equation (12.3) is called the equation of a bundle of planes.

Consider a general first-degree equation with three variables x, y and z:

Assuming that at least one of the coefficients A, B or C is not equal to zero, for example, we rewrite equation (12.4) in the form .

Comparing equation (12.5) with equation (12.3), we see that equations (12.4) and (12.5) are the equation of a plane with a normal vector passing through the point

So, equation (12.4) defines a certain plane in the Oxyz coordinate system. Equation (12.4) is called the general equation of the plane.

1. If D = 0, then it takes the form . This equation is satisfied by the point. Therefore, in this case the plane passes through the origin.

2. If C = 0, then we have the equation. The normal vector is perpendicular to the Οz axis. Consequently, the plane is parallel to the Οz axis; if B = 0 - parallel to the Oy axis, A = 0 - parallel to the Ox axis.

3. If C = D = 0, then the plane passes through parallel to the Οz axis, i.e., the plane passes through the Οz axis. Similarly, the equations correspond to planes passing through the Ox and Oy axes, respectively.

4. If A = B = 0, then equation (12.4) takes the form , i.e. The plane is parallel to the Oxy plane. Similarly, the equations and correspond to planes parallel to the planes Oyz and Οxz, respectively.

5. If A = B = D = 0, then equation (12.4) will take the form , i.e. z = 0. This is the equation of the Oxy plane. Similarly: y = 0 - equation of the Οxz plane; x = O - equation of the Oyz plane.

Equation of a plane passing through three given points

Three points in space that do not lie on the same straight line define a single plane. Let us find the equation of the plane Q passing through three given points M 1 (x 1 ; y 1 ; z 1), M 2 (x 2 ; y 2 ; z 2) and M 3 (x 3 , y 3 , z 3), not lying on the same straight line.

Let’s take an arbitrary point M(x;y;z) on the plane and compose the vectors , , . These vectors lie on the Q plane, therefore they are coplanar. We use the condition of coplanarity of three vectors (their mixed product is equal to zero), we obtain, i.e.

(12.6)

Equation (12.6) is the equation of a plane passing through three given points.

Equation of a plane in segments

Let the plane cut off the segments on the Ox, Oy and Oz axes, respectively a, b And c, i.e. passes through three points A(a;0;0), B(0;b;0) And C(0;0;c)(see Fig. 70). Substituting the coordinates of these points into equation (12.6), we obtain

Expanding the determinant, we have , i.e., or

(12.7)

Equation (12.7) is called the equation of the plane in segments on the axes. It is convenient to use when constructing a plane.

Normal plane equation

The position of the plane Q is completely determined by specifying a unit vector having the direction of the perpendicular OK, lowered to

plane from the origin, and length p this perpendicular (see Fig. 71).

Let OK = p, and α, β, g are the angles formed by the unit vector е with the Ox, Oy and Οz axes. Then . Let's take an arbitrary point M(x; y; z) on the plane and connect it to the origin. Let's form a vector. For any position of the point M on the plane Q, the projection of the radius vector onto the direction of the vector is always equal to p:, i.e. or

(12.8)

Equation (12.8) is called the normal equation of the plane in vector form. Knowing the coordinates of the vectors f and e, we rewrite equation (12.8) in the form

Equation (12.9) is called the normal equation of the plane in coordinate form.

Note that the general plane equation (12.4) can be reduced to the normal equation (12.9) in the same way as was done for the equation of a line on a plane. Namely: multiply both sides of equation (12.4) by the normalizing factor , where the sign is taken opposite to the sign of the free term D of the general equation of the plane.