The extremum point of a function is the point in the domain of definition of the function at which the value of the function takes on a minimum or maximum value. The values of the function at these points are called extrema (minimum and maximum) of the function.
Definition. Dot x1 function domain f(x) is called maximum point of the function , if the value of the function at this point is greater than the values of the function at points sufficiently close to it, located to the right and left of it (that is, the inequality holds f(x0 ) > f(x 0 + Δ x) x1 maximum.
Definition. Dot x2 function domain f(x) is called minimum point of the function, if the value of the function at this point is less than the values of the function at points sufficiently close to it, located to the right and left of it (that is, the inequality holds f(x0 ) < f(x 0 + Δ x) ). In this case, the function is said to have at the point x2 minimum.
Let's say point x1 - maximum point of the function f(x) . Then in the interval up to x1 function increases, therefore the derivative of the function is greater than zero ( f "(x) > 0 ), and in the interval after x1 the function decreases, therefore, derivative of a function less than zero ( f "(x) < 0 ). Тогда в точке x1
Let us also assume that the point x2 - minimum point of the function f(x) . Then in the interval up to x2 the function is decreasing, and the derivative of the function is less than zero ( f "(x) < 0 ), а в интервале после x2 the function is increasing, and the derivative of the function is greater than zero ( f "(x) > 0 ). In this case also at the point x2 the derivative of the function is zero or does not exist.
Fermat's theorem (a necessary sign of the existence of an extremum of a function). If the point x0 - extremum point of the function f(x) then at this point the derivative of the function is equal to zero ( f "(x) = 0 ) or does not exist.
Definition. The points at which the derivative of a function is zero or does not exist are called critical points .

Example 1. Let's consider the function.
At the point x= 0 the derivative of the function is zero, therefore the point x= 0 is the critical point. However, as can be seen on the graph of the function, it increases throughout the entire domain of definition, so the point x= 0 is not the extremum point of this function.
Thus, the conditions that the derivative of a function at a point is equal to zero or does not exist are necessary conditions for an extremum, but not sufficient, since other examples of functions can be given for which these conditions are met, but the function does not have an extremum at the corresponding point. That's why there must be sufficient evidence, allowing one to judge whether there is an extremum at a particular critical point and what kind of extremum it is - maximum or minimum.
Theorem (the first sufficient sign of the existence of an extremum of a function). Critical point x0 f(x) if, when passing through this point, the derivative of the function changes sign, and if the sign changes from “plus” to “minus”, then it is a maximum point, and if from “minus” to “plus”, then it is a minimum point.
If near the point x0 , to the left and to the right of it, the derivative retains its sign, this means that the function either only decreases or only increases in a certain neighborhood of the point x0 . In this case, at the point x0 there is no extreme.
So, to determine the extremum points of the function, you need to do the following :
- Find the derivative of the function.
- Equate the derivative to zero and determine the critical points.
- Mentally or on paper, mark the critical points on the number line and determine the signs of the derivative of the function in the resulting intervals. If the sign of the derivative changes from “plus” to “minus”, then the critical point is the maximum point, and if from “minus” to “plus”, then the minimum point.
- Calculate the value of the function at the extremum points.

Example 2. Find the extrema of the function ![]() .
.
Solution. Let's find the derivative of the function:
Let's equate the derivative to zero to find the critical points:
![]() .
.
Since for any values of “x” the denominator is not equal to zero, we equate the numerator to zero:
Got one critical point x= 3 . Let us determine the sign of the derivative in the intervals delimited by this point:
in the range from minus infinity to 3 - a minus sign, that is, the function decreases,
in the interval from 3 to plus infinity there is a plus sign, that is, the function increases.
That is, period x= 3 is the minimum point.
Let's find the value of the function at the minimum point:
Thus, the extremum point of the function is found: (3; 0), and it is the minimum point.
Theorem (the second sufficient sign of the existence of an extremum of a function). Critical point x0 is the extremum point of the function f(x) if the second derivative of the function at this point is not equal to zero ( f ""(x) ≠ 0 ), and if the second derivative is greater than zero ( f ""(x) > 0 ), then the maximum point, and if the second derivative is less than zero ( f ""(x) < 0 ), то точкой минимума.
Note 1. If at the point x0 If both the first and second derivatives vanish, then at this point it is impossible to judge the presence of an extremum based on the second sufficient criterion. In this case, you need to use the first sufficient criterion for the extremum of a function.
Remark 2. The second sufficient criterion for the extremum of a function is not applicable even when the first derivative does not exist at a stationary point (then the second derivative does not exist either). In this case, you also need to use the first sufficient sign of an extremum of a function.
Local nature of the extrema of the function
From the above definitions it follows that the extremum of a function is local in nature - it is the largest and smallest value of the function compared to nearby values.
Let's say you're looking at your earnings over a period of one year. If in May you earned 45,000 rubles, and in April 42,000 rubles and in June 39,000 rubles, then May earnings are the maximum of the earnings function compared to nearby values. But in October you earned 71,000 rubles, in September 75,000 rubles, and in November 74,000 rubles, so October earnings are the minimum of the earnings function compared to nearby values. And you can easily see that the maximum among the values of April-May-June is less than the minimum of September-October-November.
Generally speaking, on an interval a function can have several extrema, and it may turn out that some minimum of the function is greater than any maximum. So, for the function shown in the figure above, .
That is, one should not think that the maximum and minimum of a function are, respectively, its largest and smallest values on the entire segment under consideration. At the maximum point, the function has the greatest value only in comparison with those values that it has at all points sufficiently close to the maximum point, and at the minimum point it has the smallest value only in comparison with those values that it has at all points sufficiently close to the minimum point.
Therefore, we can clarify the above concept of extremum points of a function and call minimum points local minimum points, and maximum points local maximum points.
We look for the extrema of the function together

Example 3.
Solution: The function is defined and continuous on the entire number line. Its derivative ![]() also exists on the entire number line. Therefore, in this case, the critical points are only those at which, i.e. , from where and . Critical points and divide the entire domain of definition of the function into three intervals of monotonicity: . Let's select one control point in each of them and find the sign of the derivative at this point.
also exists on the entire number line. Therefore, in this case, the critical points are only those at which, i.e. , from where and . Critical points and divide the entire domain of definition of the function into three intervals of monotonicity: . Let's select one control point in each of them and find the sign of the derivative at this point.
For the interval, the control point can be: find. Taking a point in the interval, we get, and taking a point in the interval, we have. So, in the intervals and , and in the interval . According to the first sufficient criterion for an extremum, there is no extremum at the point (since the derivative retains its sign in the interval), and at the point the function has a minimum (since the derivative changes sign from minus to plus when passing through this point). Let's find the corresponding values of the function: , a . In the interval the function decreases, since in this interval , and in the interval it increases, since in this interval .
To clarify the construction of the graph, we find the points of intersection of it with the coordinate axes. When we obtain an equation whose roots are and , i.e., two points (0; 0) and (4; 0) of the graph of the function have been found. Using all the information received, we build a graph (see the beginning of the example).

Example 4. Find the extrema of the function and build its graph.
The domain of definition of a function is the entire number line, except for the point, i.e. .
To shorten the study, you can use the fact that this function is even, since  . Therefore, its graph is symmetrical about the axis Oy and the study can only be performed for the interval.
. Therefore, its graph is symmetrical about the axis Oy and the study can only be performed for the interval.
Finding the derivative ![]() and critical points of the function:
and critical points of the function:
1) 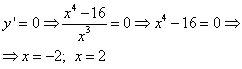 ;
;
2) ![]() ,
,
but the function suffers a discontinuity at this point, so it cannot be an extremum point.
Thus, the given function has two critical points: and . Taking into account the parity of the function, we will check only the point using the second sufficient criterion for an extremum. To do this, we find the second derivative ![]() and determine its sign at: we get . Since and , it is the minimum point of the function, and
and determine its sign at: we get . Since and , it is the minimum point of the function, and ![]() .
.
To get a more complete picture of the graph of a function, let’s find out its behavior at the boundaries of the domain of definition:
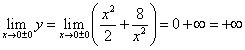
(here the symbol indicates the desire x to zero from the right, and x remains positive; similarly means aspiration x to zero from the left, and x remains negative). Thus, if , then . Next, we find
 ,
,
those. if , then .
The graph of a function has no intersection points with the axes. The picture is at the beginning of the example.
We continue to search for extrema of the function together
Example 8. Find the extrema of the function.

Solution. Let's find the domain of definition of the function. Since the inequality must be satisfied, we obtain from .
Let's find the first derivative of the function:

Let's find the critical points of the function.
Consider the graph of a continuous function y=f(x) shown in the figure.
Function value at a point x 1 will be greater than the function values at all neighboring points both to the left and to the right of x 1 . In this case, the function is said to have at the point x 1 maximum. At the point x Function 3 obviously also has a maximum. If we consider the point x 2, then the function value in it is less than all neighboring values. In this case, the function is said to have at the point x 2 minimum. Likewise for the point x 4 .
Function y=f(x) at the point x 0 has maximum, if the value of the function at this point is greater than its values at all points of some interval containing the point x 0, i.e. if there is such a neighborhood of a point x 0, which is for everyone x≠x 0 , belonging to this neighborhood, the inequality holds f(x)<f(x 0 ) .
Function y=f(x) It has minimum at the point x 0 , if there is such a neighborhood of a point x 0 , that's for everyone x≠x 0 belonging to this neighborhood, the inequality holds f(x)>f(x 0.
The points at which the function reaches its maximum and minimum are called extremum points, and the values of the function at these points are called extrema of the function.
Let us pay attention to the fact that a function defined on a segment can reach its maximum and minimum only at points contained within the segment under consideration.
Note that if a function has a maximum at a point, this does not mean that at that point the function has the greatest value in the entire domain of definition. In the figure discussed above, the function at the point x 1 has a maximum, although there are points at which the function values are greater than at the point x 1 . In particular, f(x 1) < f(x 4) i.e. the minimum of the function is greater than the maximum. From the definition of maximum it only follows that this is the largest value of the function at points sufficiently close to the maximum point.
Theorem 1. (Necessary condition for the existence of an extremum.) If the differentiable function y=f(x) has at point x= x 0 extremum, then its derivative at this point becomes zero.
Proof. Let, for definiteness, at the point x 0 function has a maximum. Then, for sufficiently small increments Δ x we have f(x 0 + Δ x)
Passing in these inequalities to the limit at Δ x→ 0 and taking into account that the derivative f "(x 0) exists, and therefore the limit on the left does not depend on how Δ x→ 0, we get: at Δ x → 0 – 0 f"(x 0) ≥ 0 a at Δ x → 0 + 0 f"(x 0) ≤ 0. Since f"(x 0) defines a number, then these two inequalities are compatible only if f"(x 0) = 0.
The proven theorem states that the maximum and minimum points can only be found among those values of the argument at which the derivative becomes zero.
We considered the case when a function has a derivative at all points of a certain segment. What is the situation in cases where the derivative does not exist? Let's look at examples.
Examples.
- y=|x|.
The function has no derivative at the point x=0 (at this point the graph of the function does not have a defined tangent), but at this point the function has a minimum, since y(0)=0, and for all x≠ 0y > 0.
- Let x< x
0 . Then c< x
0 and f "(c)> 0.
That's why f "(c)(x- x 0)<
0 and therefore
f(x) - f(x 0 )< 0, i.e. f(x)< f(x 0 ).
- Let x > x 0 . Then c>x 0 and f "(c)< 0. Means f "(c)(x- x 0)< 0. That's why f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Find the domain of a function f(x).
- Find the first derivative of a function f "(x).
- Determine critical points for this:
- find the real roots of the equation f "(x)=0;
- find all values x for which the derivative f "(x) does not exist.
- Determine the sign of the derivative to the left and right of the critical point. Since the sign of the derivative remains constant between two critical points, it is sufficient to determine the sign of the derivative at one point to the left and one point to the right of the critical point.
- Calculate the value of the function at the extremum points.
- Find all critical points of the function in the interval ( a, b) and calculate the values of the function at these points.
- Calculate the values of the function at the ends of the segment when x = a, x = b.
- From all the obtained values, select the largest and smallest.
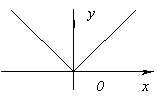
The function has no derivative at x=0, since it goes to infinity at x=0. But at this point the function has a maximum.

The function has no derivative at x=0, since ![]() at x→0. At this point the function has neither a maximum nor a minimum. Really, f(x)=0 and at x<0f(x)<0, а при x>0f(x)>0.
at x→0. At this point the function has neither a maximum nor a minimum. Really, f(x)=0 and at x<0f(x)<0, а при x>0f(x)>0.

Thus, from the examples given and the theorem formulated, it is clear that a function can have an extremum only in two cases: 1) at points where the derivative exists and is equal to zero; 2) at the point where the derivative does not exist.
However, if at some point x 0 we know that f "(x 0 ) =0, then one cannot conclude from this that at the point x 0 the function has an extremum.
For example. ![]() .
.
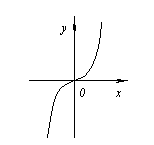
But period x=0 is not an extremum point, since to the left of this point the function values are located below the axis Ox, and on the right above.
Values of an argument from the domain of a function at which the derivative of the function vanishes or does not exist are called critical points.
From all of the above it follows that the extremum points of the function are among the critical points, and, however, not every critical point is an extremum point. Therefore, to find the extremum of a function, you need to find all the critical points of the function, and then examine each of these points separately for maximum and minimum. The following theorem serves this purpose.
Theorem 2. (Sufficient condition for the existence of an extremum.) Let the function be continuous on some interval containing the critical point x 0, and is differentiable at all points of this interval (except, perhaps, the point itself x 0). If, when moving from left to right through this point, the derivative changes sign from plus to minus, then at the point x = x 0 function has a maximum. If, when passing through x 0 from left to right, the derivative changes sign from minus to plus, then the function has a minimum at this point.
Thus, if
Proof. Let us first assume that when passing through x 0 the derivative changes sign from plus to minus, i.e. in front of everyone x, close to the point x 0 f "(x)> 0 for x< x 0 , f "(x)< 0 for x>x 0 . Let's apply Lagrange's theorem to the difference f(x) - f(x 0 ) = f "(c)(x- x 0), where c lies between x And x 0 .
Thus, for all values x close enough to x 0 f(x)< f(x 0 ) . And this means that at the point x 0 function has a maximum.
The second part of the minimum theorem is proved in a similar way.

Let us illustrate the meaning of this theorem in the figure. Let f "(x 1 ) =0 and for any x, close enough to x 1, the inequalities are satisfied
f "(x)< 0 at x< x 1 , f "(x)> 0 at x>x 1 .
Then to the left of the point x 1 the function increases and decreases on the right, therefore, when x = x 1 function goes from increasing to decreasing, that is, it has a maximum.
Similarly, we can consider points x 2 and x 3 .

All of the above can be schematically depicted in the picture:
Rule for studying the function y=f(x) for extremum
Examples. Explore functions for minimum and maximum.
MAXIMUM AND SMALLEST VALUES OF A FUNCTION ON A Segment
The largest the value of a function on an interval is the largest of all its values on this interval, and the smallest– the smallest of all its values.
Consider the function y=f(x) continuous on the segment [ a, b]. As is known, such a function reaches its maximum and minimum values, either at the boundary of the segment or inside it. If the largest or smallest value of a function is achieved at an internal point of the segment, then this value is the maximum or minimum of the function, that is, it is achieved at critical points.
Thus, we get the following rule for finding the largest and smallest values of a function on a segment[ a, b] :
To determine the nature of a function and talk about its behavior, it is necessary to find intervals of increase and decrease. This process is called function research and graphing. The extremum point is used when finding the largest and smallest values of a function, since at them the function increases or decreases from the interval.
This article reveals the definitions, formulates a sufficient sign of increase and decrease on the interval and a condition for the existence of an extremum. This applies to solving examples and problems. The section on differentiating functions should be repeated, because the solution will need to use finding the derivative.
Yandex.RTB R-A-339285-1 Definition 1
The function y = f (x) will increase on the interval x when, for any x 1 ∈ X and x 2 ∈ X, x 2 > x 1, the inequality f (x 2) > f (x 1) is satisfied. In other words, a larger value of the argument corresponds to a larger value of the function.
Definition 2
The function y = f (x) is considered to be decreasing on the interval x when, for any x 1 ∈ X, x 2 ∈ X, x 2 > x 1, the equality f (x 2) > f (x 1) is considered true. In other words, a larger function value corresponds to a smaller argument value. Consider the figure below.
Comment: When the function is definite and continuous at the ends of the interval of increasing and decreasing, that is (a; b), where x = a, x = b, the points are included in the interval of increasing and decreasing. This does not contradict the definition; it means that it takes place on the interval x.
The main properties of elementary functions of the type y = sin x are certainty and continuity for real values of the arguments. From here we get that the sine increases over the interval - π 2; π 2, then the increase on the segment has the form - π 2; π 2.
Definition 3The point x 0 is called maximum point for the function y = f (x), when for all values of x the inequality f (x 0) ≥ f (x) is valid. Maximum function is the value of the function at a point, and is denoted by y m a x .
The point x 0 is called the minimum point for the function y = f (x), when for all values of x the inequality f (x 0) ≤ f (x) is valid. Minimum functions is the value of the function at a point, and has a designation of the form y m i n .
Neighborhoods of the point x 0 are considered extremum points, and the value of the function that corresponds to the extremum points. Consider the figure below.

Extrema of a function with the largest and smallest value of the function. Consider the figure below.

The first figure says that it is necessary to find the largest value of the function from the segment [a; b ] . It is found using maximum points and is equal to the maximum value of the function, and the second figure is more like finding the maximum point at x = b.
Sufficient conditions for a function to increase and decrease
To find the maxima and minima of a function, it is necessary to apply signs of extremum in the case when the function satisfies these conditions. The first sign is considered the most frequently used.
The first sufficient condition for an extremum
Definition 4Let a function y = f (x) be given, which is differentiable in an ε neighborhood of the point x 0, and has continuity at the given point x 0. From here we get that
- when f " (x) > 0 with x ∈ (x 0 - ε ; x 0) and f " (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
- when f "(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 for x ∈ (x 0 ; x 0 + ε), then x 0 is the minimum point.
In other words, we obtain their conditions for setting the sign:
- when the function is continuous at the point x 0, then it has a derivative with a changing sign, that is, from + to -, which means the point is called a maximum;
- when the function is continuous at the point x 0, then it has a derivative with a changing sign from - to +, which means the point is called a minimum.
To correctly determine the maximum and minimum points of a function, you must follow the algorithm for finding them:
- find the domain of definition;
- find the derivative of the function on this area;
- identify zeros and points where the function does not exist;
- determining the sign of the derivative on intervals;
- select points where the function changes sign.
Let's consider the algorithm by solving several examples of finding extrema of a function.
Example 1
Find the maximum and minimum points of the given function y = 2 (x + 1) 2 x - 2 .
Solution
The domain of definition of this function is all real numbers except x = 2. First, let's find the derivative of the function and get:
y " = 2 x + 1 2 x - 2 " = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2 ) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2
From here we see that the zeros of the function are x = - 1, x = 5, x = 2, that is, each bracket must be equated to zero. Let's mark it on the number axis and get:

Now we determine the signs of the derivative from each interval. It is necessary to select a point included in the interval and substitute it into the expression. For example, points x = - 2, x = 0, x = 3, x = 6.
We get that
y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0, which means that the interval - ∞ - 1 has a positive derivative. Similarly, we find that.
y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0
Since the second interval turned out to be less than zero, it means that the derivative on the interval will be negative. The third with a minus, the fourth with a plus. To determine continuity, you need to pay attention to the sign of the derivative; if it changes, then this is an extremum point.
We find that at the point x = - 1 the function will be continuous, which means that the derivative will change sign from + to -. According to the first sign, we have that x = - 1 is a maximum point, which means we get
y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0
The point x = 5 indicates that the function is continuous, and the derivative will change sign from – to +. This means that x = -1 is the minimum point, and its determination has the form
y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24
Graphic image

Answer: y m a x = y (- 1) = 0, y m i n = y (5) = 24.
It is worth paying attention to the fact that the use of the first sufficient criterion for an extremum does not require the differentiability of the function at the point x 0, this simplifies the calculation.
Example 2
Find the maximum and minimum points of the function y = 1 6 x 3 = 2 x 2 + 22 3 x - 8.
Solution.
The domain of a function is all real numbers. This can be written as a system of equations of the form:
1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0
Then you need to find the derivative:
y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0
The point x = 0 does not have a derivative, because the values of the one-sided limits are different. We get that:
lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3
It follows that the function is continuous at the point x = 0, then we calculate
lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 0 2 + 22 3 0 - 8 = - 8
It is necessary to perform calculations to find the value of the argument when the derivative becomes zero:
1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0
1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0
All obtained points must be marked on a straight line to determine the sign of each interval. Therefore, it is necessary to calculate the derivative at arbitrary points for each interval. For example, we can take points with values x = - 6, x = - 4, x = - 1, x = 1, x = 4, x = 6. We get that
y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0
The image on the straight line looks like

This means that we come to the conclusion that it is necessary to resort to the first sign of an extremum. Let us calculate and find that
x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , then from here the maximum points have the values x = - 4 + 2 3 3 , x = 4 - 2 3 3
Let's move on to calculating the minimums:
y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3
Let's calculate the maxima of the function. We get that
y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3
Graphic image

Answer:
y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 8 27 3
If a function f " (x 0) = 0 is given, then if f "" (x 0) > 0, we obtain that x 0 is a minimum point if f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .
Example 3
Find the maxima and minima of the function y = 8 x x + 1.
Solution
First, we find the domain of definition. We get that
D(y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0
It is necessary to differentiate the function, after which we get
y " = 8 x x + 1 " = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x
At x = 1, the derivative becomes zero, which means that the point is a possible extremum. To clarify, it is necessary to find the second derivative and calculate the value at x = 1. We get:
y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x " (x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2 " x + (x + 1) 2 x " (x + 1) 4 x = = 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 · - 4 8 = - 1< 0
This means that using the 2 sufficient condition for an extremum, we obtain that x = 1 is a maximum point. Otherwise, the entry looks like y m a x = y (1) = 8 1 1 + 1 = 4.
Graphic image

Answer: y m a x = y (1) = 4 ..
Definition 5The function y = f (x) has its derivative up to the nth order in the ε neighborhood of a given point x 0 and its derivative up to the n + 1st order at the point x 0 . Then f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .
It follows that when n is an even number, then x 0 is considered an inflection point, when n is an odd number, then x 0 is an extremum point, and f (n + 1) (x 0) > 0, then x 0 is a minimum point, f (n + 1) (x 0)< 0 , тогда x 0 является точкой максимума.
Example 4
Find the maximum and minimum points of the function y y = 1 16 (x + 1) 3 (x - 3) 4.
Solution
The original function is a rational entire function, which means that the domain of definition is all real numbers. It is necessary to differentiate the function. We get that
y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)
This derivative will go to zero at x 1 = - 1, x 2 = 5 7, x 3 = 3. That is, the points can be possible extremum points. It is necessary to apply the third sufficient condition for the extremum. Finding the second derivative allows you to accurately determine the presence of a maximum and minimum of a function. The second derivative is calculated at the points of its possible extremum. We get that
y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0
This means that x 2 = 5 7 is the maximum point. Applying the 3rd sufficient criterion, we obtain that for n = 1 and f (n + 1) 5 7< 0 .
It is necessary to determine the nature of the points x 1 = - 1, x 3 = 3. To do this, you need to find the third derivative and calculate the values at these points. We get that
y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0
This means that x 1 = - 1 is the inflection point of the function, since for n = 2 and f (n + 1) (- 1) ≠ 0. It is necessary to investigate the point x 3 = 3. To do this, we find the 4th derivative and perform calculations at this point:
y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0
From what was decided above we conclude that x 3 = 3 is the minimum point of the function.
Graphic image

Answer: x 2 = 5 7 is the maximum point, x 3 = 3 is the minimum point of the given function.
If you notice an error in the text, please highlight it and press Ctrl+Enter
What is an extremum of a function and what is the necessary condition for an extremum?
The extremum of a function is the maximum and minimum of the function.
The necessary condition for the maximum and minimum (extremum) of a function is the following: if the function f(x) has an extremum at the point x = a, then at this point the derivative is either zero, or infinite, or does not exist.
This condition is necessary, but not sufficient. The derivative at the point x = a can go to zero, infinity, or not exist without the function having an extremum at this point.
What is a sufficient condition for the extremum of a function (maximum or minimum)?
First condition:
If, in sufficient proximity to the point x = a, the derivative f?(x) is positive to the left of a and negative to the right of a, then at the point x = a the function f(x) has maximum
If, in sufficient proximity to the point x = a, the derivative f?(x) is negative to the left of a and positive to the right of a, then at the point x = a the function f(x) has minimum provided that the function f(x) here is continuous.
Instead, you can use the second sufficient condition for the extremum of a function:
Let at the point x = a the first derivative f?(x) vanish; if the second derivative f??(a) is negative, then the function f(x) has a maximum at the point x = a, if it is positive, then it has a minimum.
What is the critical point of a function and how to find it?
This is the value of the function argument at which the function has an extremum (i.e. maximum or minimum). To find it you need find the derivative function f?(x) and, equating it to zero, solve the equation f?(x) = 0. The roots of this equation, as well as those points at which the derivative of this function does not exist, are critical points, i.e., values of the argument at which there can be an extremum. They can be easily identified by looking at derivative graph: we are interested in those values of the argument at which the graph of the function intersects the abscissa axis (Ox axis) and those at which the graph suffers discontinuities.
For example, let's find extremum of a parabola.
Function y(x) = 3x2 + 2x - 50.
Derivative of the function: y?(x) = 6x + 2
Solve the equation: y?(x) = 0
6x + 2 = 0, 6x = -2, x = -2/6 = -1/3
In this case, the critical point is x0=-1/3. It is with this argument value that the function has extremum. To him find, substitute the found number in the expression for the function instead of “x”:
y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50.333.
How to determine the maximum and minimum of a function, i.e. its largest and smallest values?
If the sign of the derivative when passing through the critical point x0 changes from “plus” to “minus”, then x0 is maximum point; if the sign of the derivative changes from minus to plus, then x0 is minimum point; if the sign does not change, then at point x0 there is neither a maximum nor a minimum.
For the example considered:
We take an arbitrary value of the argument to the left of the critical point: x = -1
At x = -1, the value of the derivative will be y?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (i.e. the sign is “minus”).
Now we take an arbitrary value of the argument to the right of the critical point: x = 1
At x = 1, the value of the derivative will be y(1) = 6*1 + 2 = 6 + 2 = 8 (i.e. the sign is “plus”).
As you can see, the derivative changed sign from minus to plus when passing through the critical point. This means that at the critical value x0 we have a minimum point.
Largest and smallest value of a function on the interval(on a segment) are found using the same procedure, only taking into account the fact that, perhaps, not all critical points will lie within the specified interval. Those critical points that are outside the interval must be excluded from consideration. If there is only one critical point inside the interval, it will have either a maximum or a minimum. In this case, to determine the largest and smallest values of the function, we also take into account the values of the function at the ends of the interval.
For example, let's find the largest and smallest values of the function
y(x) = 3sin(x) - 0.5x
at intervals:
So, the derivative of the function is
y?(x) = 3cos(x) - 0.5
We solve the equation 3cos(x) - 0.5 = 0
cos(x) = 0.5/3 = 0.16667
x = ±arccos(0.16667) + 2πk.
We find critical points on the interval [-9; 9]:
x = arccos(0.16667) - 2π*2 = -11.163 (not included in the interval)
x = -arccos(0.16667) – 2π*1 = -7.687
x = arccos(0.16667) - 2π*1 = -4.88
x = -arccos(0.16667) + 2π*0 = -1.403
x = arccos(0.16667) + 2π*0 = 1.403
x = -arccos(0.16667) + 2π*1 = 4.88
x = arccos(0.16667) + 2π*1 = 7.687
x = -arccos(0.16667) + 2π*2 = 11.163 (not included in the interval)
We find the values of the function at critical values of the argument:
y(-7.687) = 3cos(-7.687) - 0.5 = 0.885
y(-4.88) = 3cos(-4.88) - 0.5 = 5.398
y(-1.403) = 3cos(-1.403) - 0.5 = -2.256
y(1.403) = 3cos(1.403) - 0.5 = 2.256
y(4.88) = 3cos(4.88) - 0.5 = -5.398
y(7.687) = 3cos(7.687) - 0.5 = -0.885
It can be seen that on the interval [-9; 9] the function has the greatest value at x = -4.88:
x = -4.88, y = 5.398,
and the smallest - at x = 4.88:
x = 4.88, y = -5.398.
On the interval [-6; -3] we have only one critical point: x = -4.88. The value of the function at x = -4.88 is equal to y = 5.398.
Find the value of the function at the ends of the interval:
y(-6) = 3cos(-6) - 0.5 = 3.838
y(-3) = 3cos(-3) - 0.5 = 1.077
On the interval [-6; -3] we have the greatest value of the function
y = 5.398 at x = -4.88
smallest value -
y = 1.077 at x = -3
How to find the inflection points of a function graph and determine the convex and concave sides?
To find all the inflection points of the line y = f(x), you need to find the second derivative, equate it to zero (solve the equation) and test all those values of x for which the second derivative is zero, infinite or does not exist. If, when passing through one of these values, the second derivative changes sign, then the graph of the function has an inflection at this point. If it doesn’t change, then there is no bend.
The roots of the equation f? (x) = 0, as well as possible points of discontinuity of the function and the second derivative, divide the domain of definition of the function into a number of intervals. The convexity on each of their intervals is determined by the sign of the second derivative. If the second derivative at a point on the interval under study is positive, then the line y = f(x) is concave upward, and if negative, then downward.
How to find the extrema of a function of two variables?
To find the extrema of the function f(x,y), differentiable in the domain of its specification, you need:
1) find the critical points, and for this - solve the system of equations
fх? (x,y) = 0, fу? (x,y) = 0
2) for each critical point P0(a;b) investigate whether the sign of the difference remains unchanged
for all points (x;y) sufficiently close to P0. If the difference remains positive, then at point P0 we have a minimum, if negative, then we have a maximum. If the difference does not retain its sign, then there is no extremum at point P0.
The extrema of a function are determined similarly for a larger number of arguments.
Who is Hercules
Hercules in ancient Greek mythology is the greatest hero, the son of the god Zeus and Alcmene, the wife of the Theban king Amphitryon. At birth he was named Alcides. Repeatedly mentioned already in the Iliad (II 658, etc.). Among the numerous myths about Hercules, the most famous is the cycle of tales about the 12 labors performed
What is the name of Nigeria's money?
Country name Name - money/change coin Australia Australian dollar/cent Austria Austrian schilling/grosz - euro Azerbaijan Manat Albania Lek/kindarka Algeria Algerian dinar/centimo Argentina Argentine austral/centavo Afghanistan Afghani/pul Bangladesh Taka/pais Belgium Belgian franc/centimo - euro Bulgaria Lev/stotinka
What is yellow fever
All information is provided for informational purposes only. Only a doctor can make the correct diagnosis and prescribe appropriate treatment! Yellow fever (amaryllosis) is an acute hemorrhagic vector-borne disease of viral etiology, a tropical zooanthroponosis in Africa and South America. Transmitted by mosquito bites. Symptoms of Incubus
What songs are played in episode 12 of season 6 of Smallville?
Season 6 of Smallville has twenty episodes. Promo Music: APM Music - Dark Bells (1:55); Bloc Party - The Prayer (3:44). Episode #3: Wither: T
What is the FIFA Ferenc Puskás Award?
The FIFA Ferenc Puskas Award is an award established by FIFA on October 20, 2009. The award is given to the player (regardless of gender) who scores the most beautiful goal of the year. The award is named after the captain of the great Hungarian Golden Team of the 50s, Ferenc Puskás. First ceremony
Why is the Stone Age called "Stone Age"
In the initial period of human history, stone tools were predominantly used, which is why it is called the Stone Age. According to the modern classification, the Stone Age is divided into: the Old Stone Age, or Paleolithic, dating from the appearance of man (more than 2.5 million years BC) until approximately the 10th millennium BC. e.; Middle Stone, Mesolithic: 10th millennium
1. You can find out the owner’s details (last name, first name, patronymic) by mobile phone number by contacting security services or government agencies for help. Intelligence officers can use the data of a mobile operator in the event of capturing a criminal or solving a terrorist act. 2. You can hire a private detective. Private detectives usually "
What drugs are classified as doping agents?
The name itself - doping - comes from the English word dope - which means to give a drug. According to the definition of the Medical Commission of the International Olympic Committee, doping is the introduction into the body of athletes by any means (in the form of injections, tablets, inhalation, etc.) of pharmacological drugs that artificially increase performance and athletic performance. Except
When and by whom was the world's largest cave discovered?
The world's largest cave, Son Doong, is located in Vietnam's Phong Nha Ke Bang National Park, which is located 500 km south of the country's capital Hanoi. The length of the cave is about 9 km. Moreover, its height reaches 200 m, and its width - 150 m. The volume of the cave is estimated at 38.5 million m3. The cave was first explored in
Why is it believed that the Universe is expanding
First of all, it is necessary to emphasize that the use of the term “Universe”, as well as a discussion of its observable properties, makes sense only starting from spatial scales exceeding 100 megaparsecs, since cosmic structures such as galaxy clusters can still be traced to distances of hundreds of megaparsecs (1 parsec = 3,085&middo
Which grammatical dictionary of the Russian language is considered official in the Russian Federation
List of grammars, dictionaries and reference books containing the norms of the modern Russian literary language when used as the state language of the Russian Federation: 1. Spelling dictionary of the Russian language. Bukchina B.Z., Sazonova I.K., Cheltsova L.K. - M.: "AST-PRESS", 2008. - 128
An important concept in mathematics is function. With its help, you can visually represent many processes occurring in nature, and reflect the relationship between certain quantities using formulas, tables and images on a graph. An example is the dependence of the pressure of a layer of liquid on a body on the depth of immersion, acceleration - on the action of a certain force on an object, an increase in temperature - on the transferred energy, and many other processes. Studying a function involves constructing a graph, finding out its properties, domain of definition and values, intervals of increase and decrease. An important point in this process is finding extremum points. We will talk further about how to do this correctly.
About the concept itself using a specific example
In medicine, plotting a function graph can tell us about the progress of a disease in a patient’s body, clearly reflecting his condition. Let's assume that the OX axis represents time in days, and the OU axis represents the human body temperature. The figure clearly shows how this indicator rises sharply and then falls. It is also easy to notice special points reflecting the moments when a function, previously increasing, begins to decrease, and vice versa. These are extreme points, that is, critical values (maximum and minimum) in this case of the patient’s temperature, after which changes in his condition occur.

Tilt angle
You can easily determine from the figure how the derivative of the function changes. If the straight lines of the graph go up over time, then it is positive. And the steeper they are, the greater the value of the derivative, as the angle of inclination increases. During periods of decrease, this value takes on negative values, turning to zero at points of extremum, and the graph of the derivative in the latter case is drawn parallel to the OX axis.
Any other process should be treated in the same way. But the best way to tell about this concept is the movement of various bodies, clearly shown in the graphs.
Movement
Suppose an object moves in a straight line, uniformly picking up speed. During this period, the change in the coordinates of the body is graphically represented by a certain curve, which a mathematician would call a branch of a parabola. At the same time, the function is constantly increasing, since the coordinate indicators are changing faster and faster every second. The velocity graph shows the behavior of the derivative, the value of which also increases. This means that the movement has no critical points.
This would continue indefinitely. But what if the body suddenly decides to slow down, stop and start moving in a different direction? In this case, the coordinate indicators will begin to decrease. And the function will pass a critical value and turn from increasing to decreasing.

Using this example, you can again understand that extremum points on the graph of a function appear at the moments when it ceases to be monotonic.
Physical meaning of the derivative
What was described earlier clearly showed that the derivative is essentially the rate of change of the function. This clarification contains its physical meaning. Extremum points are critical areas on the graph. They can be identified and detected by calculating the value of the derivative, which turns out to be equal to zero.
There is another sign that is a sufficient condition for an extremum. The derivative at such inflection points changes its sign: from “+” to “-” in the maximum area and from “-” to “+” in the minimum area.

Movement under the influence of gravity
Let's imagine another situation. The children, playing with a ball, threw it in such a way that it began to move at an angle to the horizon. At the initial moment, the speed of this object was the highest, but under the influence of gravity it began to decrease, and with each second by the same amount, equal to approximately 9.8 m/s 2 . This is the value of the acceleration that occurs under the influence of earth's gravity during free fall. On the Moon it would be about six times smaller.
The graph describing the movement of a body is a parabola with branches pointing down. How to find extreme points? In this case, this is the top of the function, where the speed of the body (ball) takes zero value. The derivative of the function becomes zero. In this case, the direction, and therefore the speed value, changes to the opposite. The body flies down faster every second, and accelerates by the same amount - 9.8 m/s 2 .

Second derivative
In the previous case, the velocity modulus graph is drawn as a straight line. This line is initially directed downward, since the value of this value is constantly decreasing. Having reached zero at one point in time, then the indicators of this value begin to increase, and the direction of the graphical representation of the speed module changes dramatically. The line is now pointing upward.
Velocity, being a derivative of the coordinate with respect to time, also has a critical point. In this region, the function, initially decreasing, begins to increase. This is the location of the extremum point of the derivative of the function. In this case, the angle of inclination of the tangent becomes zero. And acceleration, being the second derivative of the coordinate with respect to time, changes sign from “-” to “+”. And the movement from uniformly slow becomes uniformly accelerated.
Acceleration graph
Now let's look at four pictures. Each of them displays a graph of changes over time in such a physical quantity as acceleration. In the case of “A” its value remains positive and constant. This means that the speed of the body, like its coordinate, is constantly increasing. If we imagine that the object will move in this way for an infinitely long time, the function reflecting the dependence of the coordinate on time will turn out to be constantly increasing. It follows from this that it has no critical regions. There are also no extremum points on the graph of the derivative, that is, linearly varying speed.

The same applies to case “B” with positive and constantly increasing acceleration. True, the graphs for coordinates and speed here will be somewhat more complicated.
When acceleration goes to zero
Looking at figure “B”, one can observe a completely different picture characterizing the movement of the body. Its speed will be graphically represented by a parabola with branches directed downward. If we continue the line describing the change in acceleration until it intersects with the OX axis and further, we can imagine that up to this critical value, where the acceleration turns out to be zero, the speed of the object will increase more and more slowly. The extremum point of the derivative of the coordinate function will be exactly at the vertex of the parabola, after which the body will radically change the nature of its movement and begin to move in a different direction.
In the last case, “G”, the nature of the movement cannot be accurately determined. Here we only know that there is no acceleration for some period under consideration. This means that the object can remain in place or move at a constant speed.
Coordinate addition problem
Let's move on to tasks that are often encountered when studying algebra at school and are offered for preparation for the Unified State Exam. The figure below shows the graph of the function. It is required to calculate the sum of extremum points.

Let's do this for the ordinate axis by determining the coordinates of the critical areas where a change in the characteristics of the function is observed. Simply put, we will find the values along the OX axis for the inflection points, and then proceed to adding the resulting terms. According to the graph, it is obvious that they take the following values: -8; -7 ; -5; -3; -2; 1; 3. This adds up to -21, which is the answer.
Optimal solution
There is no need to explain how important the choice of the optimal solution can be in performing practical tasks. After all, there are many ways to achieve a goal, but the best way out, as a rule, is only one. This is extremely necessary, for example, when designing ships, spaceships and airplanes, and architectural structures to find the optimal shape of these man-made objects.

The speed of vehicles largely depends on the proper minimization of the resistance that they experience when moving through water and air, on the overloads that arise under the influence of gravitational forces and many other indicators. A ship at sea requires such qualities as stability during a storm; for a river vessel, a minimum draft is important. When calculating the optimal design, extreme points on the graph can clearly give an idea of the best solution to a complex problem. Problems of this kind are often solved in economics, in business areas, and in many other life situations.
From ancient history
Even the ancient sages were occupied with extreme problems. Greek scientists successfully unraveled the mystery of areas and volumes through mathematical calculations. They were the first to understand that on a plane of various figures that have the same perimeter, the circle always has the largest area. Similarly, the ball is endowed with the maximum volume among other objects in space with the same surface area. Such famous personalities as Archimedes, Euclid, Aristotle, Apollonius devoted themselves to solving such problems. Heron was excellent at finding extremum points and, using calculations, built ingenious devices. These included machines moving by steam, pumps and turbines operating on the same principle.

Construction of Carthage
There is a legend, the plot of which is based on solving one of the extreme problems. The result of the business approach demonstrated by the Phoenician princess, who turned to the sages for help, was the construction of Carthage. The plot of land for this ancient and famous city was given to Dido (that was the name of the ruler) by the leader of one of the African tribes. The area of the allotment did not seem very large to him at first, since according to the contract it was supposed to be covered with oxhide. But the princess ordered her soldiers to cut it into thin strips and make a belt from them. It turned out to be so long that it covered an area where an entire city could fit.
Origins of mathematical analysis
Now let's move from ancient times to a later era. It is interesting that Kepler was prompted to understand the foundations of mathematical analysis in the 17th century by a meeting with a wine seller. The merchant was so knowledgeable in his profession that he could easily determine the volume of the drink in the barrel simply by lowering an iron rope into it. Reflecting on such a curiosity, the famous scientist managed to solve this dilemma for himself. It turns out that skillful coopers of those times got the hang of making vessels in such a way that, at a certain height and radius of the circumference of the fastening rings, they had maximum capacity.
This became a reason for Kepler to think further. The coopers came to the optimal solution through a long search, mistakes and new attempts, passing on their experience from generation to generation. But Kepler wanted to speed up the process and learn how to do the same thing in a short time through mathematical calculations. All his developments, picked up by his colleagues, turned into the now famous Fermat and Newton-Leibniz theorems.
Maximum area problem
Let's imagine that we have a wire whose length is 50 cm. How can we make a rectangle out of it that has the largest area?
When starting a decision, you should proceed from simple truths known to everyone. It is clear that the perimeter of our figure will be 50 cm. It is made up of double the lengths of both sides. This means that, having designated one of them as “X”, the other can be expressed as (25 - X).
From here we get an area equal to X(25 - X). This expression can be thought of as a function that takes multiple values. Solving the problem requires finding the maximum of them, which means you need to find out the extremum points.
To do this, we find the first derivative and equate it to zero. The result is a simple equation: 25 - 2X = 0.
From it we learn that one of the sides is X = 12.5.
Therefore, the other: 25 - 12.5 = 12.5.
It turns out that the solution to the problem will be a square with a side of 12.5 cm.

How to find maximum speed
Let's look at another example. Let's imagine that there is a body whose linear motion is described by the equation S = - t 3 + 9t 2 - 24t - 8, where the distance traveled is expressed in meters and time in seconds. We need to find the maximum speed. How to do it? Downloaded, we find the speed, that is, the first derivative.
We get the equation: V = - 3t 2 + 18t - 24. Now to solve the problem we again need to find the extremum points. This must be done in the same way as in the previous task. We find the first derivative of the speed and equate it to zero.
We get: - 6t + 18 = 0. Hence t = 3 s. This is the time when the speed of the body takes on a critical value. We substitute the resulting data into the velocity equation and get: V = 3 m/s.
But how can we understand that this is the maximum speed, since the critical points of a function can be its largest or smallest values? To check, you need to find the second derivative of the speed. It is expressed by the number 6 with a minus sign. This means that the found point is a maximum. And in the case of a positive value, the second derivative would have a minimum. This means that the solution found turned out to be correct.
The problems given as an example are only a part of those that can be solved if you know how to find the extremum points of a function. In fact, there are many more of them. And such knowledge opens up unlimited possibilities for human civilization.