In this lesson we will learn how to establish the continuity of a function. We will do this using limits, one-sided ones at that - right and left, which are not at all scary, despite the fact that they are written as and .
But what is continuity of a function anyway? Until we get to a strict definition, it's easiest to imagine a line that can be drawn without lifting the pencil from the paper. If such a line is drawn, then it is continuous. This line is the graph of a continuous function.
Graphically, a function is continuous at a point if its graph does not “break” at this point. The graph of such a continuous function is 
shown in the figure below.
Determination of continuity of a function through a limit. A function is continuous at a point if three conditions are met:
1. The function is defined at point .
If at least one of the listed conditions is not met, the function is not continuous at the point. In this case, they say that the function suffers a discontinuity, and the points on the graph at which the graph is interrupted are called discontinuity points of the function. The graph of such a function that suffers a discontinuity at the point x=2 is in the figure below.
Example 1. Function f(x) is defined as follows:
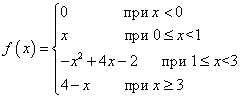
Will this function be continuous at each of the boundary points of its branches, that is, at the points x = 0 , x = 1 , x = 3 ?
Solution. We check all three conditions for the continuity of a function at each boundary point. The first condition is met, since what function defined at each of the boundary points follows from the definition of the function. It remains to check the remaining two conditions.
Dot x= 0 . Let's find the left-hand limit at this point:
.
Let's find the right-hand limit:
x= 0 must be found for that branch of the function that includes this point, that is, the second branch. We find them:
As we can see, the limit of the function and the value of the function at the point x= 0 are equal. Therefore, the function is continuous at the point x = 0 .
Dot x= 1 . Let's find the left-hand limit at this point:
Let's find the right-hand limit:
Limit of a function and value of a function at a point x= 1 must be found for that branch of the function that includes this point, that is, the second branch. We find them:
.
Limit of a function and value of a function at a point x= 1 are equal. Therefore, the function is continuous at the point x = 1 .
Dot x= 3 . Let's find the left-hand limit at this point:
Let's find the right-hand limit:
Limit of a function and value of a function at a point x= 3 must be found for that branch of the function that includes this point, that is, the second branch. We find them:
.
Limit of a function and value of a function at a point x= 3 are equal. Therefore, the function is continuous at the point x = 3 .
The main conclusion: this function is continuous at each boundary point.
Establish the continuity of a function at a point yourself, and then look at the solution
A continuous change in a function can be defined as a gradual change, without jumps, in which a small change in the argument entails a small change in the function.
Let's illustrate this continuous change in function with an example.
Let a weight hang on a thread above the table. Under the influence of this load, the thread stretches, so the distance l load from the point of suspension of the thread is a function of the mass of the load m, that is l = f(m) , m≥0 .
If you slightly change the mass of the load, then the distance l will change little: small changes m small changes correspond l. However, if the mass of the load is close to the tensile strength of the thread, then a slight increase in the mass of the load can cause the thread to break: distance l will increase abruptly and become equal to the distance from the suspension point to the table surface. Graph of a function l = f(m) shown in the figure. At a section, this graph is a continuous (solid) line, and at a point it is interrupted. The result is a graph consisting of two branches. At all points except , the function l = f(m) is continuous, but at a point it has a discontinuity.
Studying a function for continuity can be either an independent task or one of the stages of a complete study of the function and constructing its graph.
Continuity of a function on an interval
Let the function y = f(x) defined in the interval ] a, b[ and is continuous at every point of this interval. Then it is called continuous in the interval ] a, b[ . The concept of continuity of a function on intervals of the form ]- ∞ is defined similarly, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Let now the function y = f(x) defined on the interval [ a, b] . The difference between an interval and a segment: the boundary points of an interval are not included in the interval, but the boundary points of a segment are included in the segment. Here we should mention the so-called one-sided continuity: at the point a, remaining on the segment [ a, b] , we can only approach from the right, and to the point b- only on the left. The function is said to be continuous on the interval [ a, b] , if it is continuous at all interior points of this segment, continuous on the right at the point a and is left continuous at the point b.
An example of a continuous function can be any of the elementary functions. Each elementary function is continuous on any interval on which it is defined. For example, the functions and are continuous on any interval [ a, b], the function is continuous on the interval [ 0 , b] , the function is continuous on any segment not containing a point a = 2 .
Example 4. Examine the function for continuity.
Solution. Let's check the first condition. The function is not defined at points 3 and 3. At least one of the conditions for continuity of the function along the entire number line is not satisfied. Therefore, this function is continuous on the intervals
.Example 5. Determine at what value of the parameter a continuous throughout domain of definition function 
Solution.
Let's find the right-hand limit at:
.
Obviously, the value at the point x= 2 should be equal ax :
a = 1,5 .
Example 6. Determine at what parameter values a And b continuous throughout domain of definition function 
Solution.
Let's find the left-sided limit of the function at the point:
.
Therefore, the value at the point must be 1:
Let's find the left-hand function at the point:
Obviously, the value of the function at a point should be equal to:
Answer: the function is continuous over the entire domain of definition when a = 1; b = -3 .
Basic properties of continuous functions
Mathematics came to the concept of a continuous function by studying, first of all, various laws of motion. Space and time are infinite, and dependence, for example, paths s from time t expressed by law s = f(t) , gives an example of a continuous functions f(t) . The temperature of the heated water also changes continuously; it is also a continuous function of time: T = f(t) .
In mathematical analysis, some properties that continuous functions have are proven. Let us present the most important of these properties.
1. If a function continuous on an interval takes values of different signs at the ends of the interval, then at some point of this interval it takes a value equal to zero. In a more formal statement, this property is given in a theorem known as the first Bolzano-Cauchy theorem.
2. Function f(x) , continuous on the interval [ a, b] , takes all intermediate values between the values at the end points, that is, between f(a) And f(b) . In a more formal statement, this property is given in a theorem known as the second Bolzano-Cauchy theorem.
Let the point a belongs to the function specification area f(x) and any ε -neighborhood of a point a contains different from a points of the function definition area f(x), i.e. dot a is the limit point of the set (x), on which the function is specified f(x).
Definition. Function f(x) called continuous at a point a, if function f(x) has at the point a limit and this limit is equal to the particular value f(a) functions f(x) at the point a.
From this definition we have the following function continuity condition f(x) at the point a :
Since , then we can write
Therefore, for a continuous line at a point a functions the limit transition symbol and the symbol f function characteristics can be swapped.
Definition. Function f(x) is called continuous on the right (left) at the point a, if the right (left) limit of this function at the point a exists and is equal to the private value f(a) functions f(x) at the point a.
The fact that the function f(x) continuous at a point a on the right write it like this:
And the continuity of the function f(x) at the point a on the left is written as:
Comment. Points at which a function does not have the property of continuity are called discontinuity points of this function.
Theorem. Let functions be given on the same set f(x) And g(x), continuous at a point a. Then the functions f(x)+g(x), f(x)-g(x), f(x) g(x) And f(x)/g(x)- continuous at a point a(in the case of a private one, you need to additionally require g(a) ≠ 0).
Continuity of basic elementary functions
1) Power function y=xn with natural n continuous on the entire number line.
First let's look at the function f(x)=x. By the first definition of the limit of a function at a point a take any sequence (xn), converging to a, then the corresponding sequence of function values (f(x n)=x n) will also converge to a, that is 
, that is, the function f(x)=x continuous at any point on the number line.
Now consider the function f(x)=x n, Where n is a natural number, then f(x)=x · x · … · x. Let's go to the limit at x → a, we get , that is, the function f(x)=x n continuous on the number line.
2) Exponential function.
Exponential function y=a x at a>1 is a continuous function at any point on an infinite line.
Exponential function y=a x at a>1 satisfies the conditions:
3) Logarithmic function.
The logarithmic function is continuous and increasing along the entire half-line x>0 at a>1 and is continuous and decreases along the entire half-line x>0 at 0
4) Hyperbolic functions.
The following functions are called hyperbolic functions:
From the definition of hyperbolic functions it follows that the hyperbolic cosine, hyperbolic sine and hyperbolic tangent are defined on the entire numerical axis, and the hyperbolic cotangent is defined everywhere on the numerical axis, with the exception of the point x=0.
Hyperbolic functions are continuous at every point of their domain (this follows from the continuity of the exponential function and the theorem on arithmetic operations).
5) Power function
Power function y=x α =a α log a x continuous at every point of the open half-line x>0.
6) Trigonometric functions.
Functions sin x And cos x continuous at every point x an infinite straight line. Function y=tan x (kπ-π/2,kπ+π/2), and the function y=ctg x continuous on each interval ((k-1)π,kπ)(everywhere here k- any integer, i.e. k=0, ±1, ±2, …).
7) Inverse trigonometric functions.
Functions y=arcsin x And y=arccos x continuous on the segment [-1, 1] . Functions y=arctg x And y=arcctg x continuous on an infinite line.
Two wonderful limits
Theorem. Function limit (sin x)/x at the point x=0 exists and is equal to one, i.e.
This limit is called the first remarkable limit.
Proof. At 0
These inequalities are also valid for the values x, satisfying the conditions -π/2 
. Because cos x is a continuous function, then 
. Thus, for functions cos x, 1 and in some δ
-neighborhood of a point x=0 all conditions of the theorems are satisfied. Hence, 
.
Theorem. Function limit 
at x → ∞ exists and is equal to the number e:
This limit is called second remarkable limit.
Comment. It is also true that
Continuity of a complex function
Theorem. Let the function x=φ(t) continuous at a point a, and the function y=f(x) continuous at a point b=φ(a). Then the complex function y=f[φ(t)]=F(t) continuous at a point a.
Let x=φ(t) And y=f(x)- the simplest elementary functions, with many values (x) functions x=φ(t) is the scope of the function y=f(x). As we know, elementary functions are continuous at every point of the given domain. Therefore, according to the previous theorem, the complex function y=f(φ(t)), that is, the superposition of two elementary functions, is continuous. For example, a function is continuous at any point x ≠ 0, as a complex function of two elementary functions x=t -1 And y=sin x. Also function y=ln sin x continuous at any point in the intervals (2kπ,(2k+1)π), k ∈ Z (sin x>0).
1. Introduction.
2. Determination of continuity of a function.
3. Classification of break points
4. Properties of continuous functions.
5. The economic meaning of continuity.
6. Conclusion.
10.1. Introduction
Whenever we assess the inevitable changes in the world around us over time, we try to analyze the ongoing processes in order to highlight their most significant features. One of the first questions to arise along this path is: How changes characteristic of this phenomenon occur - continuously or discretely, i.e. spasmodically. Is the currency depreciating or collapsing evenly, is there a gradual evolution or a revolutionary leap? In order to unify qualitative and quantitative assessments of what is happening, one should abstract from the specific content and study the problem in terms of functional dependence. This can be done by the theory of limits, which we discussed in the last lecture.
10.2. Definition of continuity of a function
The continuity of a function is intuitively related to the fact that its graph is a continuous curve that does not break anywhere. We draw a graph of such a function without lifting our pen from the paper. If a function is given in a table, then, strictly speaking, its continuity cannot be judged, because for a given table step the behavior of the function in intervals is not defined.
In reality, with continuity, the following circumstance occurs: if the parameters characterizing the situation A little change then A little the situation will change. The important thing here is not that the situation will change, but that it will change “a little.”
Let us formulate the concept of continuity in the language of increments. Let some phenomenon be described by a function and point a belongs to the domain of definition of the function. The difference is called argument increment at the point a, difference – function increment at the point a.
Definition 10.1.Function continuous at a point a, if it is defined at this point and an infinitesimal increment in the argument corresponds to an infinitesimal increment in the function:
Example 10.1. Examine the continuity of the function at the point.
Solution. Let's build a graph of the function and mark the increments D on it x and D y(Fig. 10.1).
The graph shows that the smaller the increment D x, the less D y. Let's show this analytically. The increment of the argument is equal to , then the increment of the function at this point will be equal to
From this it is clear that if , then and:
.
Let us give another definition of the continuity of a function.
Definition 10.2.The function is called continuous at point a if:
1) it is defined at point a and some of its surroundings;
2) one-sided limits exist and are equal to each other:
;
3) limit of the function at x® a is equal to the value of the function at this point:
.
If at least one of these conditions is violated, then the function is said to undergo gap.
This definition is operational for establishing continuity at a point. Following his algorithm and noting the coincidences and discrepancies between the requirements of the definition and a specific example, we can conclude that the function is continuous at a point.
In Definition 2, the idea of proximity clearly emerges when we introduced the concept of limit. With an unlimited approximation of the argument x to the limit value a, continuous at a point a function f(x) approaches the limiting value arbitrarily close f(a).
10.3. Classification of break points
The points at which the continuity conditions of a function are violated are called break points this function. If x 0 is the break point of the function; at least one of the conditions for the continuity of the function is not satisfied. Consider the following example.
1. The function is defined in a certain neighborhood of the point a, but not defined at the point itself a. For example, the function is not defined at point a=2, therefore undergoes a discontinuity (see Fig. 10.2).
Rice. 10.2 Fig. 10.3
2. The function is defined at a point a and in some of its neighborhood, its one-sided limits exist, but are not equal to each other: 
, then the function undergoes a discontinuity. For example, the function
is defined at the point, but at the function experiences a discontinuity (see Fig. 10.3), because
And 
().
3. The function is defined at a point a and in some neighborhood of it, there is a limit of the function at , but this limit is not equal to the value of the function at the point a:
.
For example, the function (see Fig. 10.4)
Here is the breaking point:
,
All discontinuity points are divided into removable discontinuity points, discontinuity points of the first and second kind.
Definition 10.1. The break point is called the point repairable gap , if at this point there are finite limits of the function on the left and on the right, equal to each other:
.
The limit of the function at this point exists, but is not equal to the value of the function at the limit point (if the function is defined at the limit point), or the function at the limit point is not defined.
In Fig. 10.4 at the point the continuity conditions are violated, and the function has a discontinuity. Point on the graph (0; 1) gouged out. However, this gap can be easily eliminated - it is enough to redefine this function, setting it equal to its limit at this point, i.e. put . Therefore, such gaps are called removable.
Definition 10.2. The breaking point is called discontinuity point of the 1st kind , if at this point there are finite limits of the function on the left and on the right, but they are not equal to each other:
.
At this point the function is said to experience leap.
In Fig. 10.3 the function has a discontinuity of the 1st kind at the point. The left and right limits at this point are equal:
And .
The jump of the function at the discontinuity point is equal to .
It is impossible to define such a function as continuous. The graph consists of two half-lines separated by a jump.
Definition 10.3. The breaking point is called discontinuity point of the 2nd kind , if at least one of the one-sided limits of the function (left or right) does not exist or is equal to infinity.
In Figure 10.3, the function at a point has a discontinuity of the 2nd kind. The considered function at is infinitely large and has no finite limit either on the right or on the left. Therefore, there is no need to talk about continuity at such a point.
Example 10.2. Construct a graph and determine the nature of the break points:
Solution. Let's plot the function f(x) (Figure 10.5).
The figure shows that the original function has three discontinuity points: , x 2 = 1,
x 3 = 3. Let's consider them in order.
Therefore the point has rupture of the 2nd kind.
a) The function is defined at this point: f(1) = –1.
b) 
, ,
those. at the point x 2 = 1 available repairable gap. By redefining the function value at this point: f(1) = 5, the discontinuity is eliminated and the function at this point becomes continuous.
a) The function is defined at this point: f(3) = 1.
So, at the point x 1 = 3 available rupture of the 1st kind. The function at this point experiences a jump equal to D y= –2–1 = –3.
10.4. Properties of continuous functions
Recalling the corresponding properties of limits, we conclude that functions that are the result of arithmetic operations on functions continuous at the same point are also continuous. Note:
1) if the functions and are continuous at the point a, then the functions , and (provided that ) are also continuous at this point;
2) if the function is continuous at the point a and the function is continuous at the point , then the complex function is continuous at the point a And
,
those. the limit sign can be placed under the sign of a continuous function.
They say that a function is continuous on some set if it is continuous at every point of this set. The graph of such a function is a continuous line that can be crossed out with one stroke of the pen.
All major elementary functions are continuous at all points where they are defined.
Functions, continuous on the segment, have a number of important distinctive properties. Let us formulate theorems expressing some of these properties.
Theorem 10.1 (Weierstrass's theorem ). If a function is continuous on a segment, then it reaches its minimum and maximum values on this segment.
Theorem 10.2 (Cauchy's theorem ). If a function is continuous on an interval, then on this interval all intermediate values between the smallest and largest values.
The following important property follows from Cauchy's theorem.
Theorem 10.3. If a function is continuous on a segment and takes on values of different signs at the ends of the segment, then between a and b there is a point c at which the function vanishes:.
The geometric meaning of this theorem is obvious: if the graph of a continuous function goes from the lower half-plane to the upper half-plane (or vice versa), then at least at one point it will intersect the axis Ox(Fig. 10.6).
Example 10.3. Approximately calculate the root of the equation
, (i.e. approximately replace) polynomial of the corresponding degree.
This is a very important property of continuous functions for practice. For example, very often continuous functions are specified by tables (observational or experimental data). Then, using some method, you can replace the tabulated function with a polynomial. In accordance with Theorem 10.3, this can always be done with sufficiently high accuracy. Working with an analytically defined function (especially a polynomial) is much easier.
10.5. Economic meaning of continuity
Most of the functions used in economics are continuous, and this allows one to make quite significant statements of economic content.
To illustrate, consider the following example.
Tax rate N has approximately the same graph as in Fig. 10.7a.
At the ends of the intervals it is discontinuous and these discontinuities are of the 1st kind. However, the amount of income tax itself P(Fig. 10.7b) is a continuous function of annual income Q. From here, in particular, it follows that if the annual incomes of two people differ insignificantly, then the difference in the amounts of income tax that they must pay should also differ insignificantly. It is interesting that the circumstance is perceived by the vast majority of people as completely natural, which they do not even think about.
10.6. Conclusion
Toward the end, let’s allow ourselves a small retreat.
Here's how to graphically express the sad observation of the ancients:
Sic transit Gloria mundi...
(This is how earthly glory passes …)
End of work -
This topic belongs to the section:
Concept of function
The concept of function.. everything flows and everything changes Heraclitus.. table x x x x y y y y y..
If you need additional material on this topic, or you did not find what you were looking for, we recommend using the search in our database of works:
What will we do with the received material:
If this material was useful to you, you can save it to your page on social networks:
The study of a function for continuity at a point is carried out according to an already established routine scheme, which consists of checking three conditions of continuity:
Example 1
Examine the function for continuity. Determine the nature of the function discontinuities, if they exist. Execute the drawing.
Solution:
1) The only point within the scope is where the function is not defined.
One-sided limits are finite and equal.
Thus, at the point the function suffers a removable discontinuity.
What does the graph of this function look like?
I would like to simplify 
, and it seems like an ordinary parabola is obtained. BUT the original function is not defined at point , so the following clause is required:
Let's make the drawing: 
Answer: the function is continuous on the entire number line except the point at which it suffers a removable discontinuity.
The function can be further defined in a good or not so good way, but according to the condition this is not required.
You say this is a far-fetched example? Not at all. This has happened dozens of times in practice. Almost all of the site’s tasks come from real independent work and tests.
Let's get rid of our favorite modules:
Example 2
Explore function 
for continuity. Determine the nature of the function discontinuities, if they exist. Execute the drawing.
Solution: For some reason, students are afraid and don’t like functions with a module, although there is nothing complicated about them. We have already touched on such things a little in the lesson. Geometric transformations of graphs. Since the module is non-negative, it is expanded as follows: 
, where “alpha” is some expression. In this case, and our function should be written piecewise: 
But the fractions of both pieces must be reduced by . The reduction, as in the previous example, will not take place without consequences. The original function is not defined at the point since the denominator goes to zero. Therefore, the system should additionally specify the condition , and make the first inequality strict: 
Now about a VERY USEFUL decision technique: before finalizing the task on a draft, it is advantageous to make a drawing (regardless of whether it is required by the conditions or not). This will help, firstly, to immediately see points of continuity and points of discontinuity, and, secondly, it will 100% protect you from errors when finding one-sided limits.
Let's do the drawing. In accordance with our calculations, to the left of the point it is necessary to draw a fragment of a parabola (blue color), and to the right - a piece of a parabola (red color), while the function is not defined at the point itself: 
If in doubt, take a few x values and plug them into the function 
(remembering that the module destroys the possible minus sign) and check the graph.
Let us examine the function for continuity analytically:
1) The function is not defined at the point, so we can immediately say that it is not continuous at it.
2) Let’s establish the nature of the discontinuity; to do this, we calculate one-sided limits: 
The one-sided limits are finite and different, which means that the function suffers a discontinuity of the 1st kind with a jump at the point . Note that it doesn't matter whether the function at the break point is defined or not.
Now all that remains is to transfer the drawing from the draft (it was made as if with the help of research ;-)) and complete the task:
Answer: the function is continuous on the entire number line except for the point at which it suffers a discontinuity of the first kind with a jump.
Sometimes they require additional indication of the discontinuity jump. It is calculated simply - from the right limit you need to subtract the left limit: , that is, at the break point our function jumped 2 units down (as the minus sign tells us).
Example 3
Explore function 
for continuity. Determine the nature of the function discontinuities, if they exist. Make a drawing.
This is an example for you to solve on your own, a sample solution at the end of the lesson.
Let's move on to the most popular and widespread version of the task, when the function consists of three parts:
Example 4
Examine a function for continuity and plot a graph of the function
.
Solution: it is obvious that all three parts of the function are continuous on the corresponding intervals, so it remains to check only two points of “junction” between the pieces. First, let's make a draft drawing; I commented on the construction technique in sufficient detail in the first part of the article. The only thing is that we need to carefully follow our singular points: due to the inequality, the value belongs to the straight line (green dot), and due to the inequality, the value belongs to the parabola (red dot): 
Well, in principle, everything is clear =) All that remains is to formalize the decision. For each of the two “joining” points, we standardly check 3 continuity conditions:
I)
1) 
The one-sided limits are finite and different, which means that the function suffers a discontinuity of the 1st kind with a jump at the point .
Let us calculate the discontinuity jump as the difference between the right and left limits:
, that is, the graph jerked up one unit.
II) We examine the point for continuity
1) 
- the function is defined at a given point.
2) Find one-sided limits:
- one-sided limits are finite and equal, which means there is a general limit.
3) 
At the final stage, we transfer the drawing to the final version, after which we put the final chord:
Answer: the function is continuous on the entire number line, except for the point at which it suffers a discontinuity of the first kind with a jump.
Example 5
Examine a function for continuity and construct its graph 
.
This is an example for independent solution, a short solution and an approximate sample of the problem at the end of the lesson.
You may get the impression that at one point the function must be continuous, and at another there must be a discontinuity. In practice, this is not always the case. Try not to neglect the remaining examples - there will be several interesting and important features:
Example 6
Given a function 
. Investigate the function for continuity at points. Build a graph.
Solution: and again immediately execute the drawing on the draft: 
The peculiarity of this graph is that the piecewise function is given by the equation of the abscissa axis. Here this area is drawn in green, but in a notebook it is usually highlighted in bold with a simple pencil. And, of course, don’t forget about our rams: the value belongs to the tangent branch (red dot), and the value belongs to the straight line.
Everything is clear from the drawing - the function is continuous along the entire number line, all that remains is to formalize the solution, which is brought to full automation literally after 3-4 similar examples:
I) We examine the point for continuity
2) Let's calculate one-sided limits:
, which means there is a general limit.
A little funny thing happened here. The fact is that I created a lot of materials about the limits of a function, and several times I wanted to, but several times I forgot about one simple question. And so, with an incredible effort of will, I forced myself not to lose my thought =) Most likely, some “dummies” readers doubt: what is the limit of the constant? The limit of a constant is equal to the constant itself. In this case, the limit of zero is equal to zero itself (left-handed limit).
3) 
- the limit of a function at a point is equal to the value of this function at a given point.
Thus, a function is continuous at a point by the definition of continuity of a function at a point.
II) We examine the point for continuity
1) - the function is defined at a given point.
2) Find one-sided limits:
And here, in the right-hand limit, the limit of unity is equal to unity itself.
- there is a general limit.
3) 
- the limit of a function at a point is equal to the value of this function at a given point.
Thus, a function is continuous at a point by the definition of continuity of a function at a point.
As usual, after research we transfer our drawing to the final version.
Answer: the function is continuous at the points.
Please note that in the condition we were not asked anything about studying the entire function for continuity, and it is considered good mathematical form to formulate precise and clear the answer to the question posed. By the way, if the conditions do not require you to build a graph, then you have every right not to build it (although later the teacher can force you to do this).
A small mathematical “tongue twister” for solving it yourself:
Example 7
Given a function 
.
Investigate the function for continuity at points. Classify breakpoints, if any. Execute the drawing.
Try to “pronounce” all the “words” correctly =) And draw the graph more precisely, accuracy, it will not be superfluous everywhere;-)
As you remember, I recommended immediately completing the drawing as a draft, but from time to time you come across examples where you can’t immediately figure out what the graph looks like. Therefore, in some cases, it is advantageous to first find one-sided limits and only then, based on the study, depict the branches. In the final two examples we will also learn a technique for calculating some one-sided limits:
Example 8
Examine the function for continuity and construct its schematic graph.
Solution: the bad points are obvious: (reduces the denominator of the exponent to zero) and (reduces the denominator of the entire fraction to zero). It’s not clear what the graph of this function looks like, which means it’s better to do some research first:
I) We examine the point for continuity
2) Find one-sided limits:
pay attention to typical method for calculating a one-sided limit: instead of “x” we substitute . There is no crime in the denominator: the “addition” “minus zero” does not play a role, and the result is “four”. But in the numerator there is a little thriller going on: first we kill -1 and 1 in the denominator of the indicator, resulting in . Unit divided by , is equal to “minus infinity”, therefore: . And finally, the “two” in infinitely large negative degree equal to zero: . Or, to be even more specific: 
.
Let's calculate the right-hand limit:
And here - instead of “X” we substitute . In the denominator, the “additive” again does not play a role: . In the numerator, actions similar to the previous limit are carried out: we destroy the opposite numbers and divide one by : 
The right-hand limit is infinite, which means that the function suffers a discontinuity of the 2nd kind at the point .
II) We examine the point for continuity
1) The function is not defined at this point.
2) Let's calculate the left-sided limit:
The method is the same: we substitute “X” into the function. There is nothing interesting in the numerator - it turns out to be a finite positive number. And in the denominator we open the brackets, remove the “threes”, and the “additive” plays a decisive role.
As a result, the final positive number divided by infinitesimal positive number, gives “plus infinity”: .
The right-hand limit is like a twin brother, with the only exception that it appears in the denominator infinitesimal negative number:
One-sided limits are infinite, which means that the function suffers a discontinuity of the 2nd kind at the point .
Thus, we have two break points, and, obviously, three branches of the graph. For each branch, it is advisable to carry out a point-by-point construction, i.e. take several “x” values and substitute them into . Please note that the condition allows for the construction of a schematic drawing, and such relaxation is natural for manual work. I build graphs using a program, so I don’t have such difficulties, here’s a fairly accurate picture:
Direct are vertical asymptotes for the graph of this function.
Answer: the function is continuous on the entire number line except for points at which it suffers discontinuities of the 2nd kind.
A simpler function to solve on your own:
Example 9
Examine the function for continuity and make a schematic drawing.
An approximate sample solution at the end that crept up unnoticed.
See you soon!
Solutions and answers:
Example 3:Solution
: transform the function: 
. Considering the modulus disclosure rule 
and the fact that , we rewrite the function in piecewise form:
Let's examine the function for continuity.
1) The function is not defined at the point .
The one-sided limits are finite and different, which means that the function suffers a discontinuity of the 1st kind with a jump at the point . Let's make the drawing:
Answer: the function is continuous on the entire number line except the point , in which it suffers a discontinuity of the first kind with a jump. Jump Gap: (two units up).
Example 5:Solution
: Each of the three parts of the function is continuous on its own interval.
I)
1)
2) Let's calculate one-sided limits:
, which means there is a general limit.
3)
- the limit of a function at a point is equal to the value of this function at a given point.
So the function continuous at a point by defining the continuity of a function at a point.
II)
We examine the point for continuity
1) - the function is defined at a given point. the function suffers a discontinuity of the 2nd kind at the point
How to find the domain of a function?
Examples of solutions
If something is missing somewhere, it means there is something somewhere
We continue to study the “Functions and Graphs” section, and the next station on our journey is Function Domain. An active discussion of this concept began in the first lesson. about function graphs, where I looked at elementary functions, and, in particular, their domains of definition. Therefore, I recommend that dummies start with the basics of the topic, since I will not dwell on some basic points again.
It is assumed that the reader knows the domains of definition of the basic functions: linear, quadratic, cubic functions, polynomials, exponential, logarithm, sine, cosine. They are defined on . For tangents, arcsines, so be it, I forgive you =) Rarer graphs are not immediately remembered.
The scope of definition seems to be a simple thing, and a logical question arises: what will the article be about? In this lesson I will look at common problems of finding the domain of a function. Moreover, we will repeat inequalities with one variable, the solution skills of which will also be required in other problems of higher mathematics. The material, by the way, is all school material, so it will be useful not only for students, but also for students. The information, of course, does not pretend to be encyclopedic, but here are not far-fetched “dead” examples, but roasted chestnuts, which are taken from real practical works.
Let's start with a quick dive into the topic. Briefly about the main thing: we are talking about a function of one variable. Its domain of definition is many meanings of "x", for which exist meanings of "players". Let's look at a hypothetical example: 
The domain of definition of this function is a union of intervals:
(for those who forgot: - unification icon). In other words, if you take any value of “x” from the interval , or from , or from , then for each such “x” there will be a value “y”.
Roughly speaking, where the domain of definition is, there is a graph of the function. But the half-interval and the “tse” point are not included in the definition area, so there is no graph there.
Yes, by the way, if anything is not clear from the terminology and/or content of the first paragraphs, it is better to return to the article Graphs and properties of elementary functions.
Determining the continuity of a function at a point
Function f (x) called continuous at point x 0
neighborhood U (x0) this point, and if the limit as x tends to x 0
exists and is equal to the value of the function at x 0
:
.
This implies that x 0 - this is the end point. The function value in it can only be a finite number.
Definition of continuity on the right (left)
Function f (x) called continuous on the right (left) at point x 0
, if it is defined on some right-sided (left-sided) neighborhood of this point, and if the right (left) limit at the point x 0
equal to the function value at x 0
:
.
Examples
Example 1
Using the Heine and Cauchy definitions, prove that the function is continuous for all x.
Let there be an arbitrary number. Let us prove that the given function is continuous at the point.
The function is defined for all x .
Therefore, it is defined at a point and in any of its neighborhoods.
.
We use Heine's definition
.
Let's use . Let there be an arbitrary sequence converging to: .
Applying the property of the limit of a product of sequences we have:
Since there is an arbitrary sequence converging to , then
Continuity has been proven.
We use the Cauchy definition .
Let's use .
.
Let's consider the case.
;
We have the right to consider the function on any neighborhood of the point. .
Therefore we will assume that
;
(A1.1) .
.
Let's apply the formula:
.
Taking into account (A1.1), we make the following estimate:
.
.
.
(A1.2)
Applying (A1.2), we estimate the absolute value of the difference:
(A1.3)
According to the properties of inequalities, if (A1.3) is satisfied, if and if , then .
Now let's look at the point.
In this case
This means that the function is continuous at the point.
In a similar way, one can prove that the function , where n is a natural number, is continuous on the entire real axis. .
Let's use .
Example 2 .
Using prove that the function is continuous for all .
.
The given function is defined at .
.
Let us prove that it is continuous at the point.
.
Let's consider the case.
.
Let us prove that it is continuous at the point.
We have the right to consider the function on any neighborhood of the point. .
Therefore we will assume that
.
(A2.1)
(A2.2)
.
(A1.2)
Let's put it.
.
Then
.
This shows that for any positive there is always .
.
Then for all x such that , the following inequality holds:
It means that . That is, the function is continuous on the right at the point.
In a similar way, one can prove that the function , where n is a natural number, is continuous for .
References:
O.I. Besov. Lectures on mathematical analysis. Part 1. Moscow, 2004.
L.D. Kudryavtsev. Course of mathematical analysis. Volume 1. Moscow, 2003.
