Любой вектор ā можно разложить по координатным векторам, т.е. представить в виде: Нулевой вектор можно представить в виде: Координаты равных векторов соответственно равны, т.е., если ā { x 1 ; y 1 ; z 1 } = b { x 2 ; y 2 ; z 2 }, то x 1 = x 2, y 1 = y 2, z 1 = z 2.
На уроке познакомились с прямоугольной системой координат, научились строить точку по заданным ее координатам и находить координаты точки, изображенной в заданной системе координат. Декартова система координат не единственная. К следующему уроку найти в Интернете другие системы координат.
Самостоятельная работа 1 вариант 1. Даны векторы а {2; -4; 3} и b {-3; 1/2; 1}. Найдите координаты вектора с = a + b. 2. Даны векторы а {1; -2; 0}, b {3; -6; 0}, c {0; -3; 4}. Найдите координаты вектора p = 2a – 1/3b – c. 3. Найдите значения m и n, при которых векторы а {6; n; 1} и b {m; 16; 2} коллинеарны. 2 вариант 1. Даны векторы а {1; -3; -1} и b {-1; 2; 0}. Найдите координаты вектора с = a – b. 2. Даны векторы а {2; 4; -6}, b {-3; 1; 0}, c {3; 0; -1}. Найдите координаты вектора p = -1/2a + 2b – c. 3. Найдите значения m и n, при которых векторы а {-4; m; 2} и b {2; -6; n} коллинеарны.
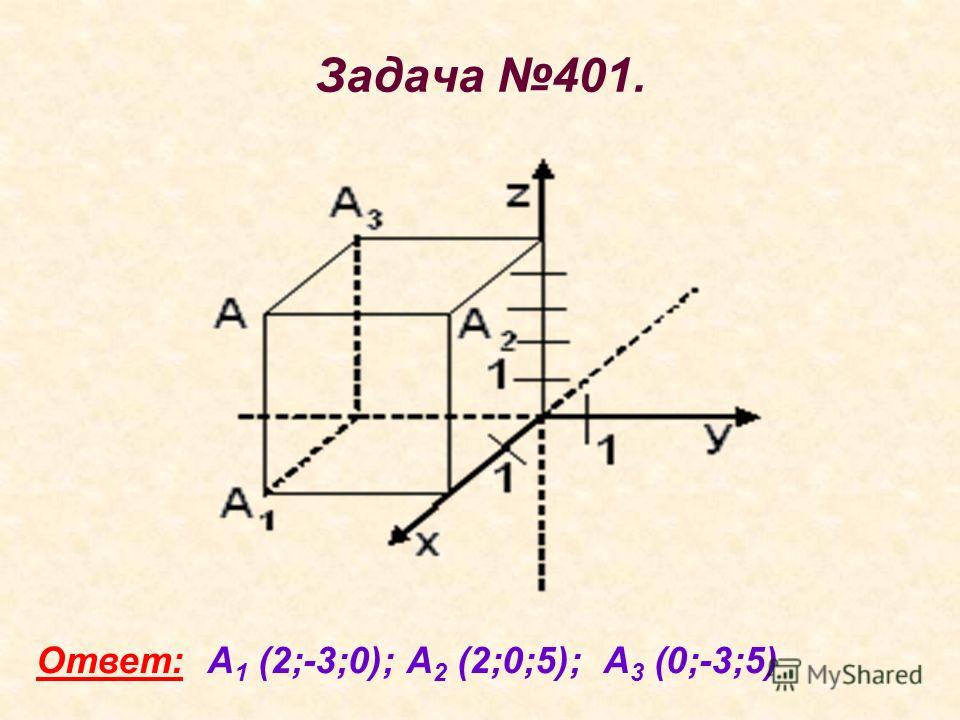
Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус- вектором данной точки. Координаты любой точки равны соответствующим координатам её радус-вектора. М (x; y; z) OM (x; y; z) A (x 1 ; y 1 ; z 1), B (x 2 ; y 2 ; z 2) AB (x 2 – x 1 ; y 2 – y 1 ; z 2 – z 1)
Государственное образовательное учреждение
начального профессионального образования
«Профессиональное училище №5» г. Белгорода
Конспект урока
по математике на тему:
Прямоугольная система координат в пространстве
для учащихся 11 классов
Подготовила:
Кобзева Ирина Алексеевна,
преподаватель информатики и математики
ГОУ НПО ПУ №5
Белгород 2010
Тема урока : Прямоугольная система координат в пространстве. Координаты вектора
Цели урока: - развить логическое и пространственное мышление
Ввести понятие системы координат в пространстве, координат вектора
Литература: Геометрия 10-11 класс Л. С. Атанасян, М.: Просвещение, 2006 год
Ход урока:
Орг. Момент
Объявление темы и цели урока.
Объяснение нового материала
Прямоугольная система координат в пространстве.
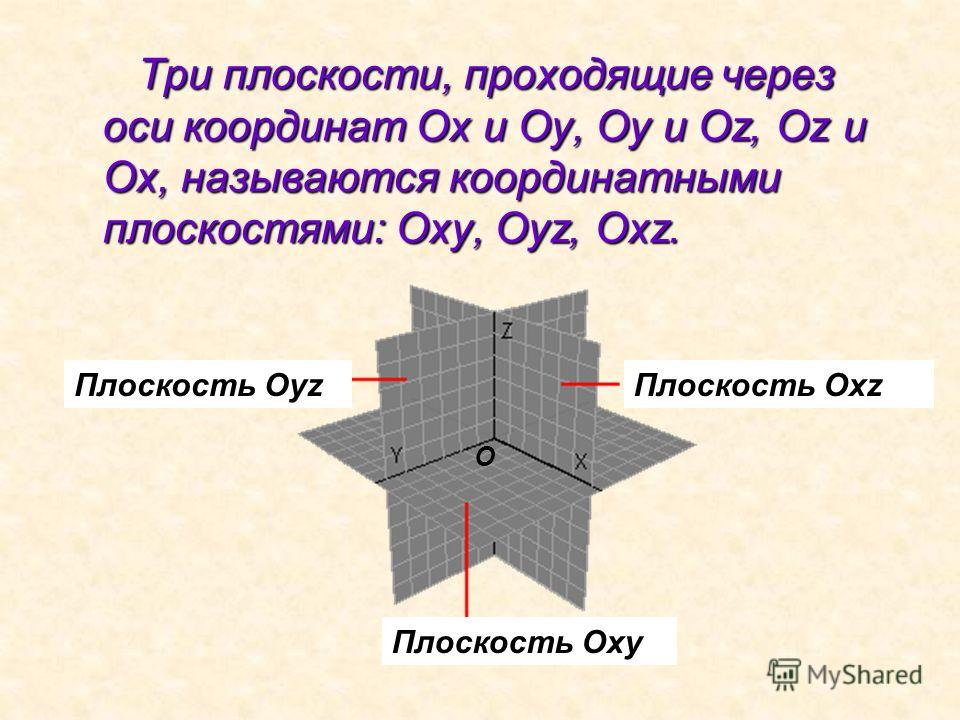
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве (рис. 121). Прямые с выбранными на них направлениями называются осями координат , а их общая точка - началом координат . Она обозначается обычно буквой О. Оси координат обозначаются так: Ох, Оу, О z - и имеют названия: ось абсцисс, ось ординат, ось аппликат. Вся система координат обозначается Охуz. Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью , а другой луч отрицательной полуосью .
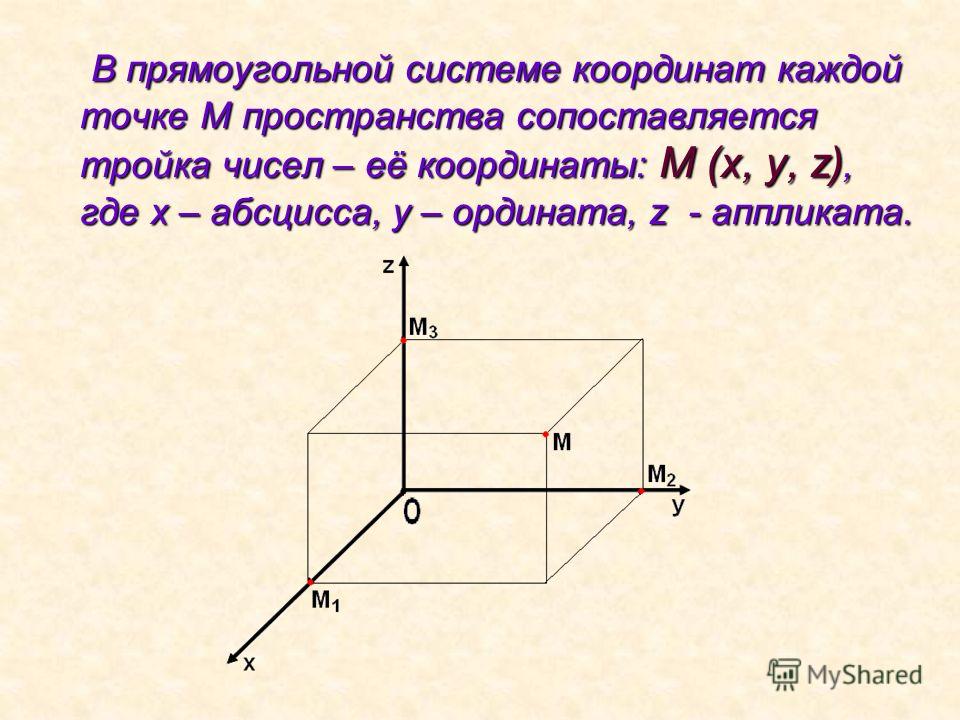
В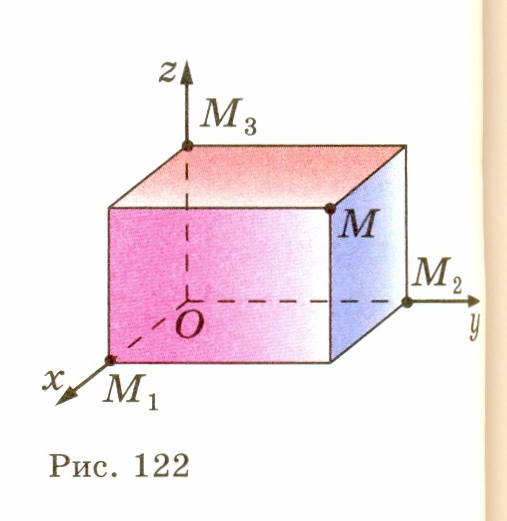
прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами
. Они определяются аналогично координатам точек на плоскости. Проведем через точку М три плоскости, перпендикулярные к осям координат, и обозначим через М 1 , М 2 и М 3 точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат (рис. 122). Первая координата точки М (она называется абсциссой
и обозначается обычно буквой х) определяется так: х = ОМ 1 , если М 1 точка положительной полуоси; х = - ОМ 1 , если М 1 точка отрицательной полуоси; х = 0, если М 1 совпадает с точкой О. Аналогично с помощью точки М 2 определяется вторая координата (ордината
)
y точки М, а с помощью точки М 3 третья координата (аппликата
) z точки М. Координаты точки М записываются в скобках после обозначения точки: М (х; у; z), причем первой указывают абсциссу, второй ординату, третьей - аппликату. На рисунке 123 изображены шесть точек А (9; 5; 10), В (4; -3; 6), С (9; 0; 0), Е (4; 0; 5), Е (0; 3; 0), F (0; 0; -3).
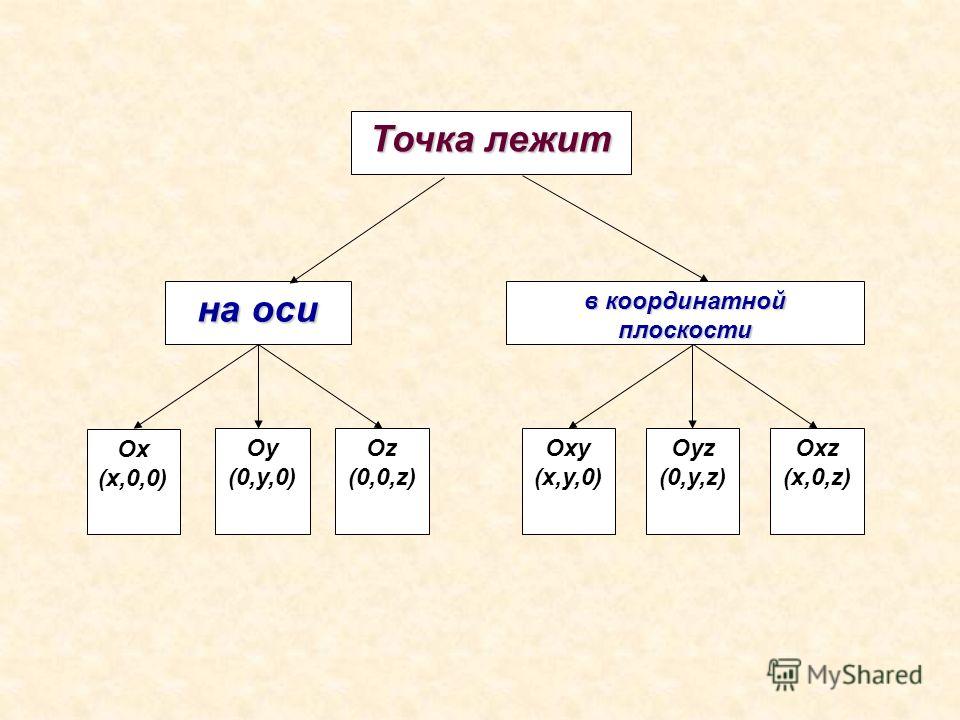
Е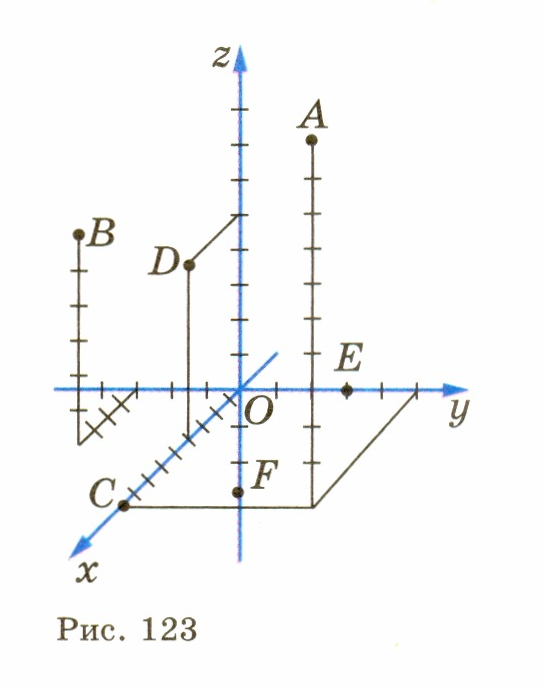
сли точка М (х; у;
z) лежит на координатной плоскости или на оси координат, то некоторые ее координаты равны нулю. Так, если М € Оху, то аппликата точки М равна нулю: z = 0. Аналогично если М с Охz, то у = 0, а если М € Оуz, то х= 0. Если М € Ох, то ордината и аппликата точки М равны нулю: у = 0 и z= 0 (например, у точки С на рисунке 123). Если М € Оу, то х = 0 и z=0; если М€ Оz, то х = 0 и у = 0. Все три координаты начала координат равны нулю: 0 (0; 0; 0).
Координаты вектора
З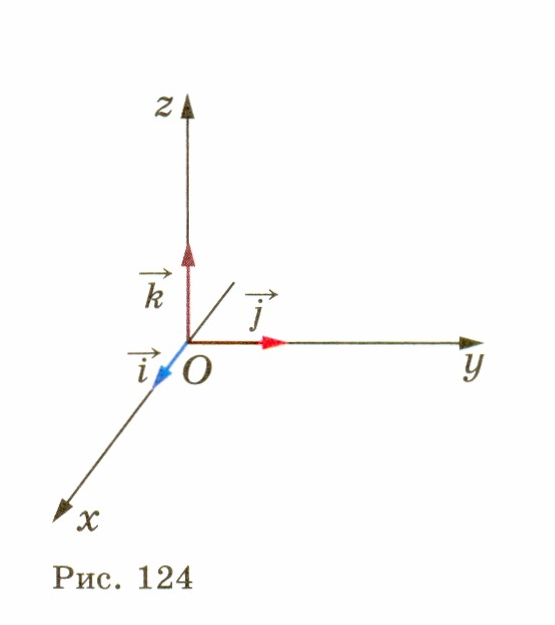
ададим в пространстве прямоугольную систему координат Оху
z. На каждой из положительных полуосей отложим от начала координат единичный вектор
, т. е. вектор, длина которого равна единице. Обозначим через i
единичный вектор оси абсцисс, через j
- единичный вектор оси ординат и через k
единичный вектор оси аппликат (рис. 124). Векторы i, j, k назовем координатными векторами
. Очевидно, эти векторы не компланарны. Поэтому любой вектор
a
и можно разложить по координатным векторам, т. е. представить в виде
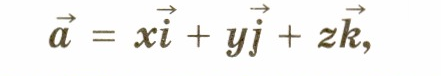
причем коэффициенты разложения х, у, z определяются единственным образом.
К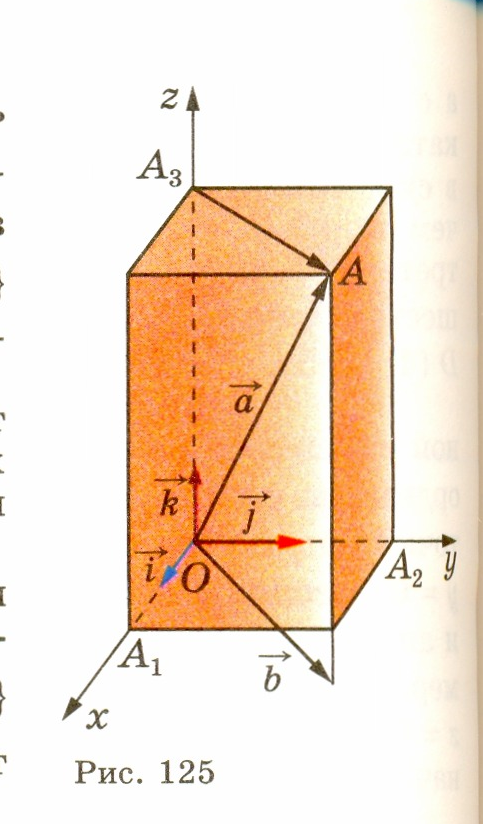
оэффициенты х, у и
z в разложении вектора a по координатным векторам называются координатами вектора
a
в данной системе координат
. Координаты вектора a будем записывать в фигурных скобках после обозначения вектора: a {х; у; z}. На рисунке 125 изображен прямоугольный параллелепипед, имеющий следующие измерения: ОА 1 = 2, ОА 2 = 2, ОА 3 =4. Координаты векторов, изображенных на этом рисунке, таковы: a {2; 2; 4}, b{2; 2; -1}, А 3 А {2; 2; 0}, i{1; 0; 0}, j{0; 1; 0}, k{0; 0; 1}.
Так как нулевой вектор можно представить в виде 0 = о i+ оj+ 0k то все координаты нулевого вектора равны нулю. Далее, координаты равных векторов соответственно равны , т. е. если векторы a{х 1 , y 1 , z 1 } и b{х 2, y 2 , z 2) равны, то х 1 = x 2 , y 1 = y 2 и z 1 = z 2 (объясните почему).
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.
1 0 . Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если a {х 1 , у 1 , z 1 } и b{х 2 , у 2 , z 2 } - данные векторы, то вектор a+b имеет координаты {х 1 +х 2 , у 1 + у 2 , z 1 + z 2 }.
2 0 . Каждая координата разности двух векторов равна разности соответствующих координат этих векторов . Другими словами, если a {х 1 , y 1 , z 1} и b{х 2 у 2 ; z 2 } - данные векторы, то вектор a- b имеет координаты {х 1 - х 2 , y 1 – y 2 , z 1 - z 2 }.
3 О . Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если а {х; у; х} - данный вектор, α - данное число, то вектор α a имеет координаты {αх; αу; αz).
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление и выбран единица измерения отрезков, то говорят задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями наз. осями координат .(Ох, Оу, Оz )
Плоскости, проходящие соответственно через оси координат наз. координатными плоскостями.(Оху, Оуz, Оzх )
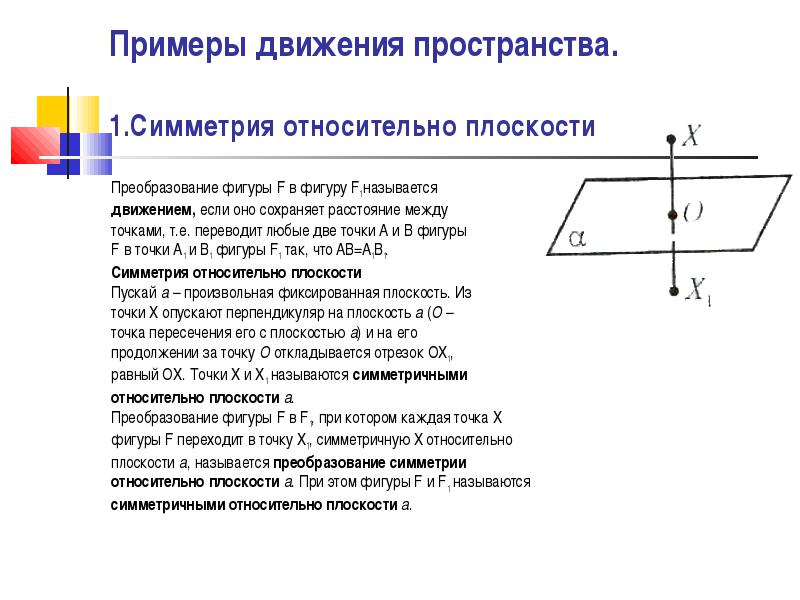
Преобразование фигуры F в фигуру F1 называется
движением, если оно сохраняет расстояние между
точками, т.е. переводит любые две точки А и В фигуры
F в точки A1 и В1 фигуры F1 так, что AB=A1B1.
Симметрия относительно плоскости
Пускай а – произвольная фиксированная плоскость. Из
точки Х опускают перпендикуляр на плоскость а (О –
точка пересечения его с плоскостью а ) и на его
продолжении за точку О откладывается отрезок ОХ1,
равный ОХ. Точки Х и Х1 называются симметричными
относительно плоскости а .
Преобразование фигуры F в F1, при котором каждая точка Х
фигуры F переходит в точку Х1, симметричную Х относительно
плоскости а , называется преобразование симметрии
относительно плоскости а . При этом фигуры F и F1 называются
симметричными относительно плоскости а .
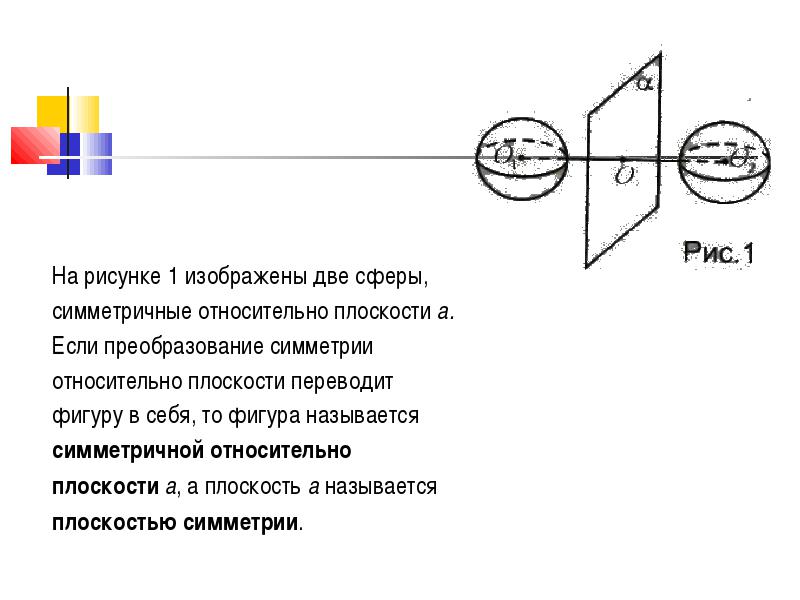
На рисунке 1 изображены две сферы,
симметричные относительно плоскости а.
Если преобразование симметрии
относительно плоскости переводит
фигуру в себя, то фигура называется
симметричной относительно
плоскости а , а плоскость а называется
плоскостью симметрии .
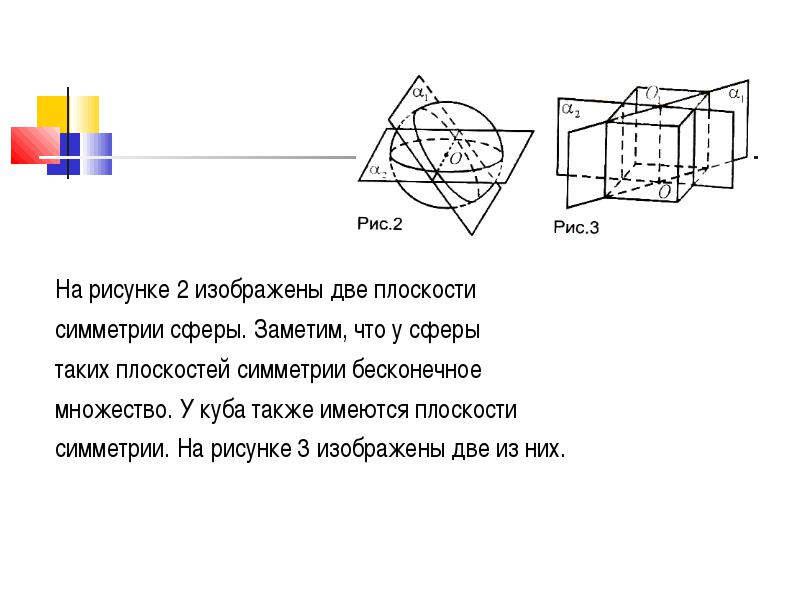
На рисунке 2 изображены две плоскости
симметрии сферы. Заметим, что у сферы
таких плоскостей симметрии бесконечное
множество. У куба также имеются плоскости
симметрии. На рисунке 3 изображены две из них.
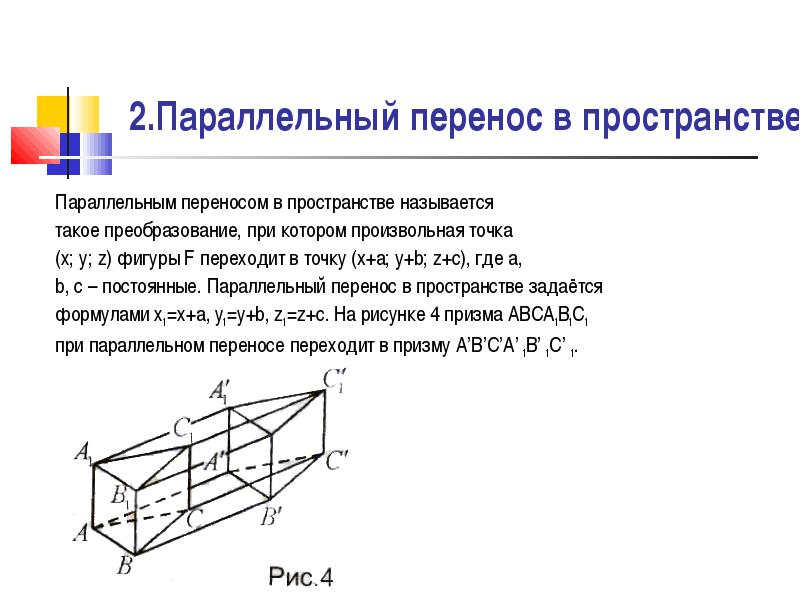
Параллельным переносом в пространстве называется
такое преобразование, при котором произвольная точка
(х; у; z) фигуры F переходит в точку (x+a; y+b; z+c), где a,
b, c – постоянные. Параллельный перенос в пространстве задаётся
формулами х1=х+а, у1=у+b, z1=z+c. На рисунке 4 призма ABCA1B1C1
при параллельном переносе переходит в призму A’B’C’A’ 1B’ 1C’ 1.
Сформулируем некоторые свойства параллельного переноса:
Параллельные перенос есть движение.
При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
При параллельном переносе прямая переходит в параллельную прямую (или в себя).
Каковы бы ни были две точки А и А1, существует, и притом единственный, параллельный перенос, при котором точка А переходит в точку А1.
При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскостью.
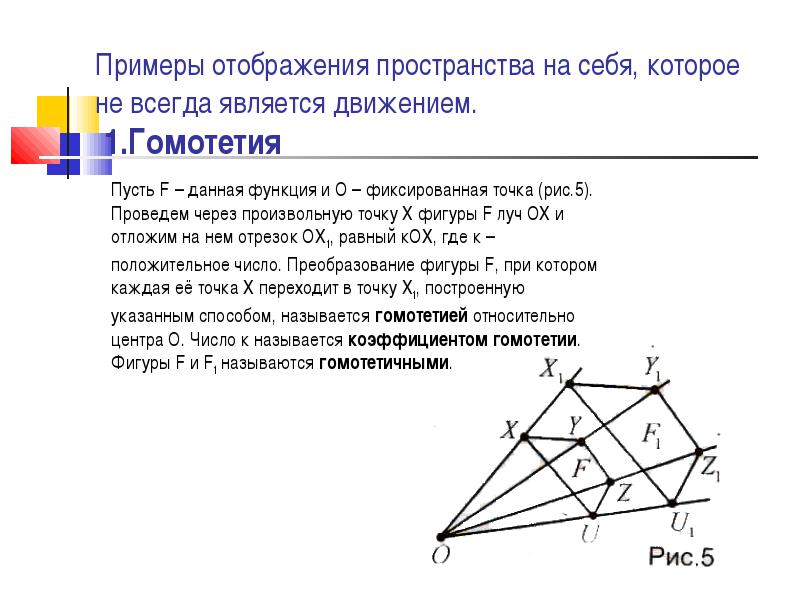
Пусть F – данная функция и О – фиксированная точка (рис.5).
Проведем через произвольную точку Х фигуры F луч ОХ и
отложим на нем отрезок ОХ1, равный кОХ, где к –
положительное число. Преобразование фигуры F, при котором
каждая её точка Х переходит в точку Х1, построенную
указанным способом, называется гомотетией относительно
центра О. Число к называется коэффициентом гомотетии .
Фигуры F и F1 называются гомотетичными .
Преобразование фигуры в фигуру называется
преобразование подобия, если при этом
преобразовании расстояния между точками
изменяются (увеличиваются или уменьшаются)
в одно и тоже число раз. Это значит, что если
произвольные точки А и В фигуры F при этом
преобразовании переходят в точки А1 и В1
фигуры F1, то А1В1=кАВ, где к >0.
Число к называется коэффициентом подобия . При
к=1 преобразование подобия является движением .
Углом между плоскостями α и β ,
Углом между плоскостями α и β ,
которые пересекаются по
прямой с, называется угол
между прямыми, по которым
третья плоскость γ,
перпендикулярна линии
пересечения, пересекает
плоскости α и β.
Угол между параллельными
плоскостями считается равным 00.
Угол между плоскостями не
превышает 900.
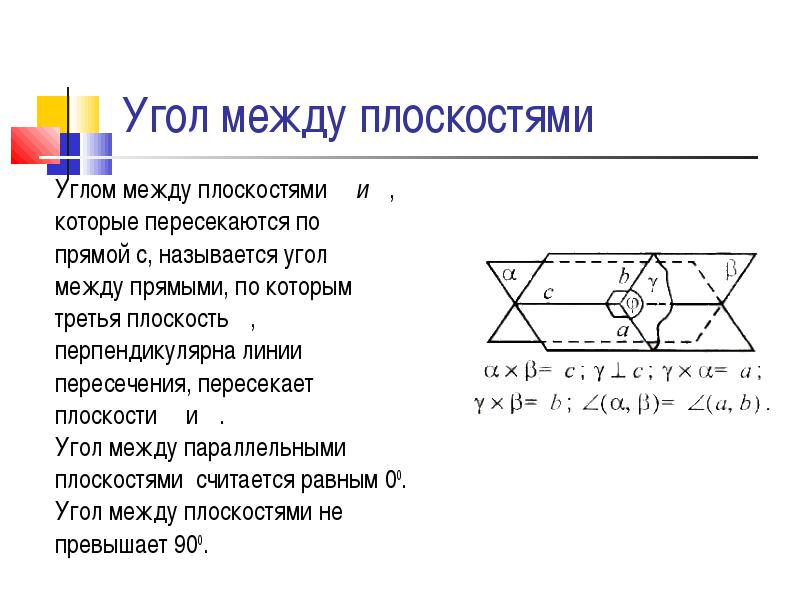
На прямой с пересечения плоскостей α и β выбираем точку С; через С плоскостях
α и β проводим прямые a и b, перпендикулярные с. Угол между прямыми a и b равен углу между плоскостями.
а ; А принадлежит с β : АВ перпендикулярно с ; АА1 перпендикулярно β а и β по определению.
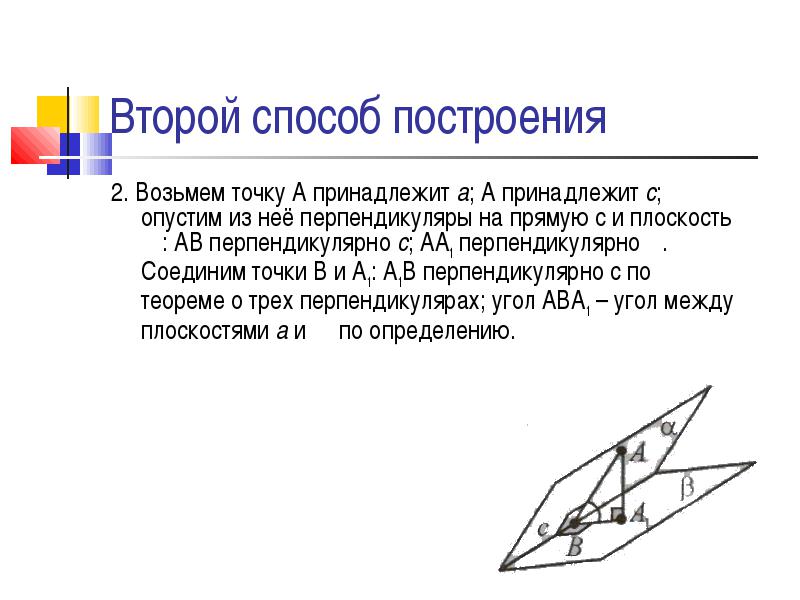
2. Возьмем точку А принадлежит а ; А принадлежит с ; опустим из неё перпендикуляры на прямую с и плоскость β : АВ перпендикулярно с ; АА1 перпендикулярно β . Соединим точки В и А1: А1В перпендикулярно с по теореме о трех перпендикулярах; угол АВА1 – угол между плоскостями а и β по определению.
Углом между прямой и плоскостью, которая её
пересекает, называется угол между этой прямой и её
проекцией на плоскость.
Для построения проекции прямой а на плоскость достаточно
найти две точки поверхности: например, точку пересечения
прямой а и плоскости и основание любого перпендикуляра,
опущенного из второй точки прямой а на плоскость.
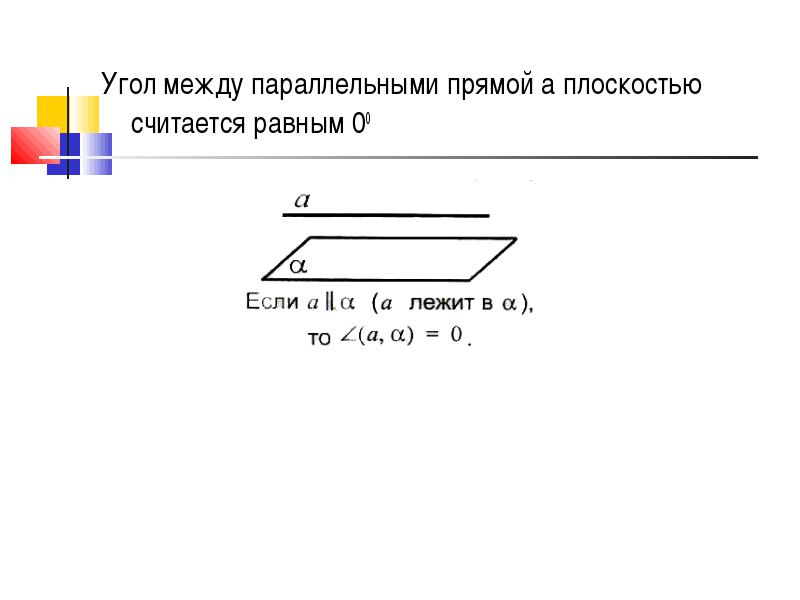
Угол между параллельными прямой а плоскостью α считается равным 00
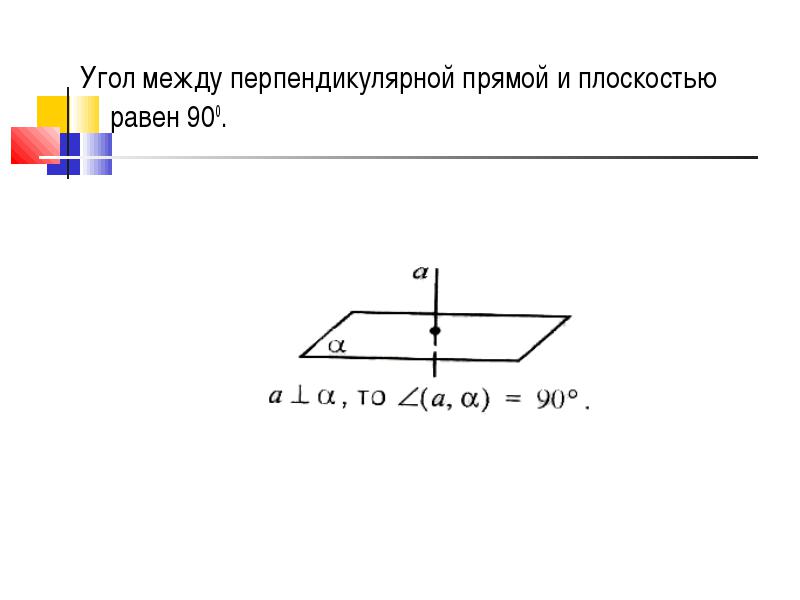
Угол между перпендикулярной прямой и плоскостью равен 900.
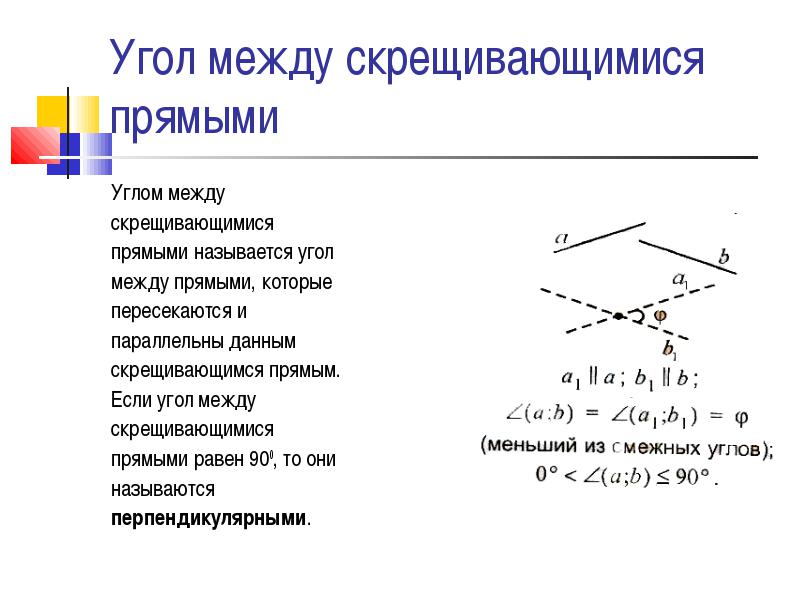
Углом между
Углом между
скрещивающимися
прямыми называется угол
между прямыми, которые
пересекаются и
параллельны данным
скрещивающимся прямым.
Если угол между
скрещивающимися
прямыми равен 900, то они
называются
перпендикулярными .
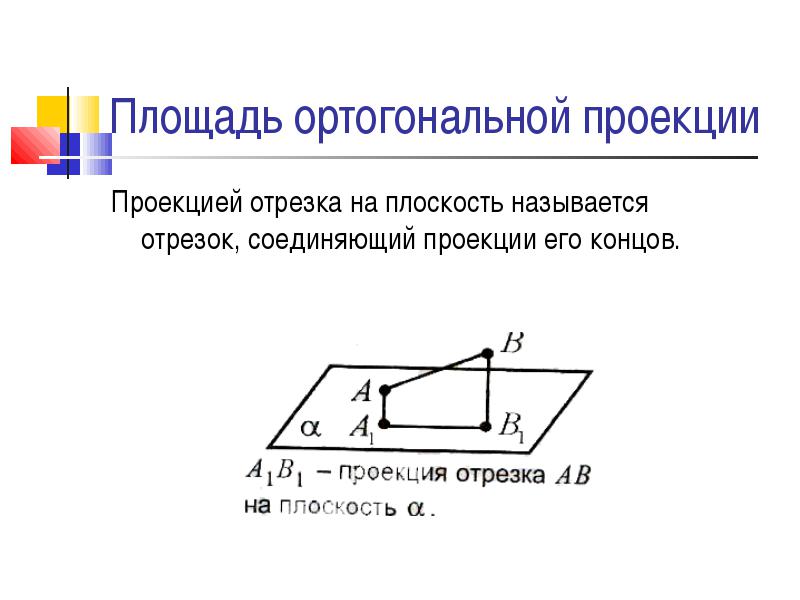
Ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на плоскость
Проекцией отрезка на плоскость называется отрезок, соединяющий проекции его концов.
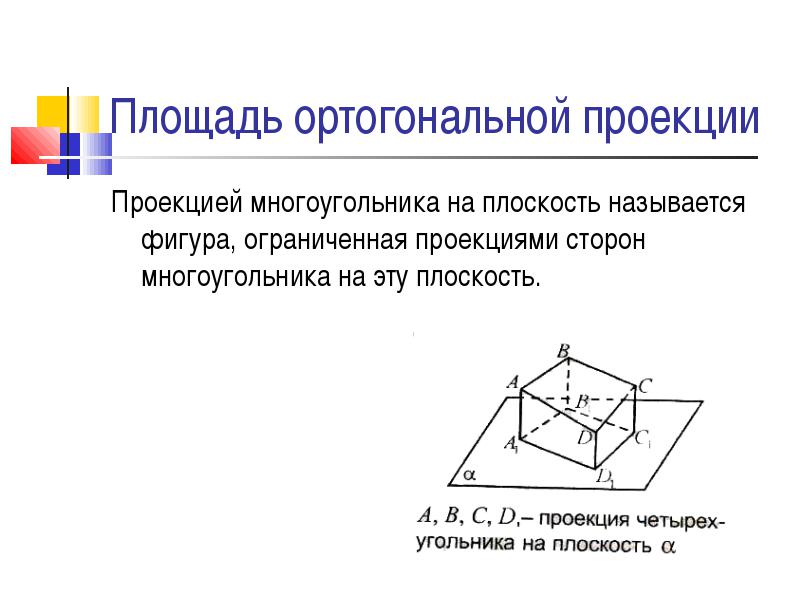
Проекцией многоугольника на плоскость называется фигура, ограниченная проекциями сторон многоугольника на эту плоскость.
Площадь ортогональной проекции многоугольника равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.
