Полярная система координат (полярные координаты)

Полярная система координат на плоскости - это совокупность точки O , называемой полюсом , и полупрямой OX , называемой полярной осью . Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор \vec{i} , приложенный к точке O , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).

Положение точки M в полярной системе координат определяется расстоянием r (полярным радиусом ) от точки M до полюса (т.е. r=\vert\overrightarrow{OM}\vert ) и углом \varphi (полярным углом ) между полярной осью и вектором \overrightarrow{OM} . Полярный радиус и полярный угол составляют полярные координаты точки M , что записывается в виде M(r,\varphi) . Полярный угол измеряется в радианах и отсчитывается от полярной оси:

В положительном направлении (против направления движения часовой стрелки), если значение угла положительное;

В отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения r\geqslant0 . Полярный угол \varphi определен для любой точки плоскости, за исключением полюса O , и принимает значения -\pi<\varphi\leqslant\pi , называемыми главными значениями полярного угла . В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых 2\pi n , где n\in\mathbb{Z} . В этом случае значениям \varphi+2\pi n полярного угла для всех n\in\mathbb{Z} соответствует одно и то же направление радиус-вектора.

С полярной системой координат Or\varphi можно связать прямоугольную систему координат O\vec{i}\vec{j} , начало O которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) - с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат {связанную с данной прямоугольной).

Выведем формулы, связывающие между собой прямоугольные координаты x,y точки M , отличной от точки O , и ее полярные координаты r,\varphi . По рис.2.28,б получаем

\begin{cases}x=r\cdot\cos\varphi,\\y=r\cdot\sin\varphi.\end{cases}

Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:

\left\{\begin{aligned}r&= \sqrt{x^2+y^2},\\ \cos\varphi&= \frac{x}{r}=\frac{x}{\sqrt{x^2+y^2}},\\ \sin\varphi&= \frac{y}{r}=\frac{y}{\sqrt{x^2+y^2}}.\end{aligned}\right.

Последние два равенства определяют полярный угол с точностью до слагаемых 2\pi n , где n\in\mathbb{Z} . При x\ne0 из них следует, что \operatorname{tg}\frac{y}{x} \varphi~(-\pi<\varphi\leqslant\pi) находится по формулам (рис.2.29):

\varphi=\left\{\begin{aligned}\operatorname{arctg}\frac{y}{x},\quad&x>0,\\\pi+\operatorname{arctg}\frac{y}{x},\quad&x<0,\,y\geqslant0,\\-\pi+\operatorname{arctg}\frac{y}{x},\quad&x<0,\,y<0,\\\frac{\pi}{2},\quad&x=0,\,y>0,\\-\frac{\pi}{2},\quad&x=0,\,y<0.\end{aligned}\right.

Пример 2.9. В полярной системе координат Or\varphi :

а) изобразить координатные линии r=1,~r=2,~r=3,~\varphi=\frac{\pi}{4},~\varphi=\frac{\pi}{2} ;

б) изобразить точки M_1,~M_2 с полярными координатами r_1=3,~\varphi_1=\frac{9\pi}{4},~r_2=3,~\varphi=-\frac{7\pi}{4} . Найти главные значения полярных углов этих точек;

в) найти прямоугольные координаты точек M_1,~M_2 .

Решение. а) Координатные линии r=1,~r=2,~r=3 представляют собой окружности соответствующих радиусов, а линии \varphi=\frac{\pi}{4}, \varphi=\frac{\pi}{2} и \varphi=\frac{3\pi}{4} - полупрямые (рис.2.30,а).

б) Построим точки M_1\!\left(3,\frac{9\pi}{4}\right) и M_2\!\left(3,-\frac{7\pi}{4}\right) (рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение \varphi=\frac{\pi}{4} . Следовательно, это одна и та же точка, которая совпадает с точкой M\!\left(3,\frac{\pi}{4}\right) , изображенной на рис.2.30,а.

в) Учитывая пункт "б", найдем прямоугольные координаты точки M . По формулам (2.17) получаем:

x=r\cdot\cos\varphi=3\cdot\cos\frac{\pi}{4}=\frac{3\sqrt{2}}{2};~y=r\cdot\sin\frac{\pi}{4}=\frac{3\sqrt{2}}{2}, то есть M\!\left(\frac{3\sqrt{2}}{2},\frac{3\sqrt{2}}{2}\right).

Замечания 2.8

1. Главное значение полярного угла можно выбрать иначе, например, 0\leqslant\varphi<2\pi .

2. Расстояние между двумя точками M_1(r_1,\varphi_1) и M_2(r_2,\varphi_2) (длина отрезка M_1M_2 ) вычисляется по формуле

M_1M_2=\sqrt{r_1^2+r_2^2-2\cdot r_1\cdot r_2\cdot\cos(\varphi_2-\varphi_1)},

что следует из теоремы косинусов (рис.2.31).

3. Ориентированная площадь S_{\ast}^{\land} параллелограмма (рис.2.31), построенного на радиус-векторах и , находится по формуле

S_{\ast\overrightarrow{OM_1},\overrightarrow{OM_2}}^{\land}=\overrightarrow{OM_1}\land\overrightarrow{OM_2}=r_1\cdot r_2\cdot\sin(\varphi_2-\varphi_1).

Она положительна, если \varphi_1<\varphi_2 (при этом ориентация пары радиус- векторов \overrightarrow{OM_1} и \overrightarrow{OM_2} правая), и отрицательна, если \varphi_1>\varphi_2 (ориентация пары радиус-векторов \overrightarrow{OM_1} и \overrightarrow{OM_2} левая).

Пример 2.10. Даны полярные координаты \varphi_A=\frac{\pi}{3},~r_A=4 и \varphi_B=\frac{2\pi}{3},~r_B=2 точек A и B (рис.2.32). Требуется найти:

а) скалярное произведение \bigl\langle\overrightarrow{OA},\overrightarrow{OB}\bigl\rangle ;

б) длину отрезка AB ;

в) внешнее произведение \overrightarrow{OA}\land\overrightarrow{OB} ;

г) площадь S_{OAB} треугольника OAB ;

д) координаты середины C отрезка AB в прямоугольной системе координат, связанной с данной полярной.

Решение. а) По определению скалярного произведения находим

\left\langle\overrightarrow{OA},\overrightarrow{OB}\right\rangle=\left|\overrightarrow{OA}\right|{\cdot}\left|\overrightarrow{OB}\right|\!\cdot\cos\psi=r_A\cdot r_B\cdot\cos(\varphi_B-\varphi_A)=4\cdot2\cdot\cos\frac{\pi}{3}=4.

б) Находим длину отрезка (см. пункт 2 замечаний 2.8):

AB=\sqrt{r_A^2+r_B^2-2\cdot r_A\cdot r_B\cdot\cos(\varphi_B-\varphi_A)}=\sqrt{4^2+2^2-2\cdot4\cdot2\cdot\frac{1}{2}}=2\sqrt{3}.

в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и :

\overrightarrow{OA}\land\overrightarrow{OB}=r_A\cdot r_B\cdot\sin(\varphi_B-\varphi_A)=2\cdot4\cdot\sin\frac{\pi}{3}=4\sqrt{3}.

Площадь положительная, так как векторы \overrightarrow{OA} и \overrightarrow{OB} образуют правую пару (\varphi_A<\varphi_B) .

г) Площадь треугольника OAB находим как половину площади параллелограмма, построенного на радиус-векторах \overrightarrow{OA} и \overrightarrow{OB} .

Так как S_{\ast\overrightarrow{OA},\overrightarrow{OB}}=\left|\overrightarrow{OA}\land\overrightarrow{OB}\right|=4\sqrt{3} (см. пункт "в"), то S_{OAB}=\frac{1}{2}\cdot4\sqrt{3}=2\sqrt{3} .

д) По формулам (2.17) находим прямоугольные координаты точек A и B :

\begin{gathered}x_A=r_A\cdot\cos\varphi_A=4\cdot\frac{1}{2}=2,\quad y_A=r_A\cdot\sin\varphi_A=4\cdot\frac{\sqrt{3}}{2}=2\sqrt{3};\\ x_B=r_B\cdot\cos\varphi_B=2\cdot\frac{-1}{2}=-1,\quad y_B=r_B\cdot\sin\varphi_B=2\cdot\frac{\sqrt{3}}{2}=\sqrt{3}.\end{gathered}

а затем координаты середины C отрезка AB (см. пункт 3 замечаний 2.1):

x_C=\frac{x_A+x_b}{2}=\frac{2+(-1)}{2}=\frac{1}{2};\quad y_C=\frac{y_A+y_B}{2}=\frac{2\sqrt{3}+\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}.

Пример 2.11. На координатной плоскости Oxy отмечена точка A(4,-3) . Найти:

а) полярные координаты точки A" , образа точки A при повороте радиус-вектора \overrightarrow{OA} на угол \frac{\pi}{3} вокруг начала координат (рис.2.33);

б) полярные координаты точки A_1 , образа точки A при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).

Решение. а) Найдем полярные координаты точки A . По формулам (2.17), учитывая рис.2.29, получаем:

r_A=\sqrt{x_A^2+y_A^2}=\sqrt{4^2+(-3)^2}=5;\quad\varphi_A=\operatorname{arctg}\frac{y_A}{x_A}=\operatorname{arctg}\frac{-3}{4}=-\operatorname{arctg}\frac{3}{4},

так как точка A лежит в \text{IV} четверти.

При повороте радиус-вектора \overrightarrow{OA} вокруг полюса на угол \frac{\pi}{3} полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки A" : r_{A"}=r_{A}=5 , \varphi_{A"}=\varphi_{A}+\frac{\pi}{3}=\frac{\pi}{3}-\operatorname{arctg}\frac{3}{4} , причем \varphi_{A"} - главное значение полярного угла (-\pi<\varphi_{A"}\leqslant\pi) .

б) При инверсии относительно окружности радиуса R полярные координаты r",\varphi" образа выражаются через полярные координаты r,\varphi прообраза следующими формулами:

r"=\frac{R^2}{r},\quad\varphi"=\varphi.

Поэтому, учитывая пункт "а", находим (для R=1 ):

r_{A_1}=\frac{1}{r_A}=\frac{1}{5},\quad\varphi_{A_1}=\varphi_{A}=-\operatorname{arctg}\frac{3}{4}.

Cтраница 1

Y-координаты любой точки в первом квадранте положительны.

Точки в третьем и четвертом квадрантах имеют отрицательные Y-координаты, причем в третьем квадранте Х - координаты точек отрицательны.

Координатное табло отображает точные Х - и Y-координаты текущего местоположения курсора ArchiCAD в используемой системе координат.

Во втором квадранте Х - координаты точек положительны, а Y-координаты отрицательны.

Трудность состоит в том, что расположение ферзей определяется только их Y-координатами, а Х - координаты в представлении позиции не присутствуют в явном виде.

При поиске решения программа, приведенная на рис. 4.7, проверяет различные значения Y-координат ферзей. В каком месте программы задается порядок перебора альтернативных вариантов.

Так как принято записывать вначале Х - координату точки, а затем уже Y-координату, то выражение - r - / Q - P еще не определяет нужной величины. Результат равен частному от деления разности координат по оси X на разность значений координат по оси Y, что в соответствии с определением дает величину, обратную к значению наклона прямой.

ЗНАЧЕНИЯ КООРДИНАТ) и помещает ее в выходную таблицу сообщений и в выходной список данных. Впоследствии эта команда, содержащая Х - и Y-координаты выбранной позиции экрана, будет передана в основную ЭВМ.

Положение новой системы XOt Y относительно старой системы хОу будет определено, если известны координаты а и Ь нового начала О, по старой системе и угол а между осями Ох и OtX. Обозначим через х и у координаты произвольной точки М относительно старой системы, через X и Y-координаты той же точки относительно новой системы. Наша задача заключается в том, чтобы старые координаты х и у выразить через новые X и Y. В полученные формулы преобразования должны, очевидно, входить постоянные а, Ъ и ос. Решение этой общей задачи мы получим из рассмотрения двух частных случаев.

Она ссылается на два элемента в списке данных - X и Y. Дисплейный процессор нашего терминала имеет отдельные команды для перевода луча в новое положение по Х - и Y-координатам. Поэтому процедура исполнения команды SET ORIGIN должна генерировать две команды дисплейного процессора. Кроме того, необходимо определить, какой объект инициализируется с помощью команды SET ORIGIN - сегмент или элемент. Для этого процедура опрашивает корреляционную таблицу, используя поле параметра команды. В случае сегмента позиция на экране задается в абсолютных координатах, в случае элемента - в относительных. Процедура, исполняющая команду SET ORIGIN, должна установить или очистить специальный бит соответствующих команд дисплейного процессора.

Программа будет бесконечно долго обследовать эту бесконечную область пространства, так и не приблизившись к цели. Пространство состояний задачи о восьми ферзях, определенное так, как это сделано в настоящем разделе, на первый взгляд содержит ловушку именно такого рода. Но оказывается, что оно все-таки конечно, поскольку Y-координаты выбираются из ограниченного множества, и поэтому на доску можно поставить безопасным образом не более восьми ферзей.

Процедура, исполняющая данную команду, предоставляет четыре вида средств для интерактивной генерации объектов. Первым средством является обобщенная процедура рисования прямых линий. Рисование осуществляется перемещением специальной метки в начало линии и последующим перемещением ее в конец линии. При перемещении метки в конец линии генерируется вектор, соединяющий начало линии и текущее положение метки. Освободив клавишу на корпусе светового пера, можно переместить метку с одного конца рисуемой линии на другой. Когда пользователь укажет на световую кнопку ACCEPT, генерируется команда L4, с помощью которой X, Y-координаты нарисованной линии передаются в основную ЭВМ.

Страницы: 1

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси OY вверх, ось OX смотрела направо.

Четыре угла (I, II, III, IV), образованные осями координат X"X и Y"Y, называются координатными углами или квадрантами

Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y - длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y"Y и X"X соответственно. Координата x называется абсциссой точки A, координата y - ординатой точки A. Записывают так: .

Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX - ось абсцисс, OY - ось ординат, OZ - ось аппликат.

Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси.

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y - длине отрезка OC, координата z - длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y - ординатой точки A, координата z - аппликатой точки A. Записывают так: .

Опр . Система координат (О; , , ) наз. прямоугольной, если:1) базисные векторы имеют единичную длину: = = =1;

2)базисные векторы попарно ортогональны (перпендикулярны): ⏊ ⏊ .

базисные векторы при этом обычно обозначают наз. базисными ортами, а координаты обозначают х,у, z. Оси координат называют: Ох-осью абсцисс, Оу - осью ординат, Оz-осью аппликат.

Теорема. Длина вектора =(X,Y,Z) равна корню из суммы квадратов его координат: | |= .

Док-во . Вектор представляется диагональю прямоугольного параллелепипеда со сторонами Х , .

Длины сторон параллелепипеда равны |Х|,|У|,|Z|.квадрат длины диагонали прямоугольного парал. равен сумме квадратов длин его сторон(нужно дважды применить теорему Пифагора). Отсюда получается искомая формула.

Следствие. расстояние между точками А() и В() равно АВ= .

Док-во . АВ=| |, а =().

13.Величина проекции вектора на ось. Направляющие косинусы .

Ось - это прямая, на которой выбрано направление. Пусть направление на оси задается единичным вектором .

Пусть -произвольный вектор и пусть А΄ и В΄ -ортогональные проекции точек А и В на прямую l. Вектор наз. проекцией вектора на ось l.

Опр . Величиной проекции вектора на ось l наз. координата вектора на прямой l относительно базисного вектора , т.е. такое число , что = , .

Таким образом, мы различаем проекцию вектора на ось и величину проекции вектора на ось: первое-это вектор, а второе – число. При параллельном переносе вектора вектора также параллельно сдвигается на оси l. Поэтому величина проекции вектора не зависит от выбора представителя вектора . Также величина проекции суммы векторов равна сумме их величин проекции.

Теорема. Величина проекции вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью: =| |cosφ,где φ=<().

Док-во. рассмотрим два случая:1)уголφ-острый,2)уголφ-тупой.

Направляющие косинусы.

Пусть α,β,γ –углы, которые вектор =(X,Y,Z)составляет с осями координат. Косинусы этих углов,cosα, cosβ,cosγ наз. направляющими косинусами вектора .

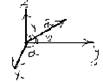α=<(Ox. ); β=<(Oy ); γ=<(Oz, .