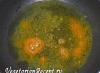
Опр.20 Совокупность фиксированной точки О и ортонормированного базиса ( ; ) называется декартовой (или прямоугольной) системой координат на плоскости. Точка О называется началом координат. Прямые Ох и Oу, проходящие через начало координат в направлении базисных векторов и (Рис.13), называются осями координат : Ox - ось абсцисс , Оу - ось ординат . Систему координат будем обозначать O или хOу, а плоскость с соответствующей системой координат будем называть плоскостью Оху.
Легко увидеть, что декартова система координат на плоскости задается двумя взаимно перпендикулярными прямыми - осями, на каждой из которых выбрано положительное направление и задан отрезок единичной длины. Оси координат делят плоскость на четыре области – четверти или квадранты .
Четверти нумеруются против часовой стрелки, как на рис.13.
Рассмотрим произвольную точку М плоскости Oxу (Рис.13). Радиус-вектором точки М по отношению к точке О называется вектор , соединяющий начало координат с данной точкой.
Координатами точки М в системе координат O называются координаты радиус-вектора в базисе ( ; ). Если =(х; у ), то координаты точки М записывают так: М(х; у ), число х называется абсциссой точки М, у - ординатой точки М.
Координаты точки могут быть найдены как проекции радиус-вектора на каждую из осей, х= а х =Пр ох и у=а у =Пр оу , =(а х; а у).
Обратно: если М(х; у ), то =(х; у ).
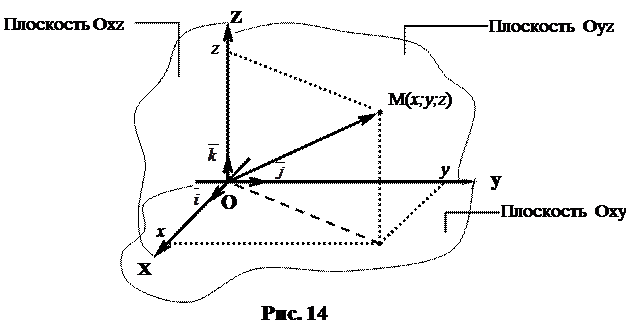 Опр.21
Совокупность фиксированной точки О и ортонормированного базиса ( ; ; ) называется декартовой
(или прямоугольной) системой координат в пространстве размерности n=3.
Опр.21
Совокупность фиксированной точки О и ортонормированного базиса ( ; ; ) называется декартовой
(или прямоугольной) системой координат в пространстве размерности n=3.
Как и на плоскости, точка О называется началом координат . Прямые Ох, Оу и Оz, проходящие через начало координат в направлении базисных векторов , , (Рис. 14), называются осями координат :
Ox – ось абсцисс , Оу – ось ординат , Oz – ось аппликат .
Плоскости, проходящие через оси координат, называются координатными плоскостями . Они делят пространство на восемь областей - октантов . Координатами точки М называются координаты радиус-вектора в базисе ( ; ; ), при этом если =(х; у; z ), то пишут М(х; у; z ), где х - абсцисса, у - ордината, z - аппликата точки М.
Обратно: если М(х; у; z ), то =(х; у; z ).
Прямоугольная система координат в пространстве дает возможность установить взаимно однозначное соответствие между точками пространства и упорядоченными тройками чисел (их координатами), а на плоскости - между точками плоскости и упорядоченными парами чисел.
В декартовой системе координат упорядоченная пара чисел одновременно задает как точку данной плоскости, так и радиус-вектор этой точки и целое множество равных ему векторов. Аналогично и в трёхмерном случае. В дальнейшем будем задавать векторы не двумя точками (начальной и конечной) а только конечной с указанием её координат. Считаем начальной точкой всех векторов (если противное не оговорено отдельно) точку О – начало координат.
Аналогично рассмотренным случаям n=2 и n=3 можно ввести понятие декартовой системы координат n-мерного пространства, которое можно обозначить R
n . Точки такого пространства, как и векторы, задаются указанием упорядоченного набора n чисел ![]() - её декартовых координат.
- её декартовых координат.
Действия над векторами в координатной форме
Пусть в декартовой системе координат Охуz даны векторы
=x 1 × +y 1 × +z 1 × и =x 2 × +y 2 × +z 2 × ,
т.е. =(x 1 ; y 1 ; z 1) и =(x 2 ; y 2 ; z 2) .
декартовыми, если отдельно не оговорено противное.
С такими векторами можно выполнить следующие действия:
сравнение, сумма (разность), умножение на число, скалярное произведение, найти модуль вектора, угол между векторами и проверить векторы на коллинеарность. Рассмотрим их подробнее:
Сравнение
Два вектора равны тогда и только тогда, когда равны все их одноименные координаты , = (х 1 = х 2 , y 1 =y 2 , z 1 =z 2).
Нарушение хотя бы одного равенства говорит о неравенстве векторов, .
Векторы различных размерностей несравнимы.
Операции “ < “ и “ > ” на векторах не заданы;
7.2 Сумма и разность векторов :
координаты суммы (разности) двух векторов равны сумме (разности)
одноименных координат этих векторов,
± =(x 1 × +y 1 × +z 1 × ) ± (x 2 × +y 2 × +z 2 × )= (х 1 ±х 2)× +(y 1 ±y 2)× +(z 1 ±z 2)× ,
(x 1 ; y 1 ; z 1) ± (x 2 ; y 2 ; z 2) = (x 1 ±x 2 ; y 1 ±y 2 ; z 1 ±z 2);
7.3 При умножении вектора на число на это число умножаются все его
координаты, l× =l×(x 1 +y 1 +z 1 )=(lх 1)× +(ly 1)× +(lz 1)× ,
l×(x 1 ; y 1 ; z 1)= (l×x 1 ; l×y 1 ; l×z 1);
7.4 Скалярное произведение двух векторов в координатной форме:
(8) × =х 1 ×x 2 +y 1 ×y 2 + z 1 ×z 2 ,
т. е. скалярное произведение двух векторов равно сумме попарных
произведений одноименных координат.
Выведем эту формулу:
× =(x 1 +y 1 +z× )×(x 2 +y 2 +z× )=
= х 1 x 2 × 2 + x 1 y 2 × × + x 1 z 2 × +
+ y 1 x 2 × × + y 1 y 2 × 2 + y 1 z 2 × +
+ z 1 x 2 × + z 1 y 2 × + z 1 z 2 × 2 .
Векторы , , ортонормированны,
т.е. для них × = × = = = = = 0, 2 = 2 = 2 =1 ,
поэтому × =х 1 x 2 × 1+y 1 y 2 × 1+ z 1 z 2 × 1;
Модуль вектора
При = формула (8) примет вид × = 2 = x 1 2 +y 1 2 +z 1 2 , –
Определение 2.8. Три взаимно перпендикулярные оси в пространстве с общим началом О и одинаковой масштабной единицей образуют декартову систему координат в пространстве . Оси занумерованы в определенном порядке и называются: первая – ось Ох или ось абсцисс , вторая – ось Оу или ось ординат , третья – ось Оz или ось аппликат .
Пусть М – произвольная точка в пространстве, а , и – проекции этой точки на оси Ох , Оу и Оz, соответственно (см. рис. 2.2).
Определение 2.9. Декартовыми координатами точки М называются алгебраические величины векторов , и . Это обозначается следующим образом: М (х , у , z ), где , , (рис. 2.2). Декартовы координаты х , у и z точки М называют еще ее абсциссой, ординатой и аппликатой , соответственно.
Определение 2.10. Пусть в пространстве дан вектор а = . Декартовыми координатами вектора а называются проекции , и этого вектора на координатные оси (см. рис. 2.3). Обозначение: а = .
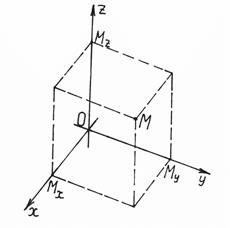
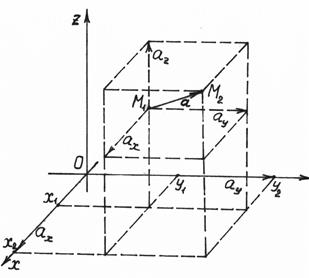
Рис. 2.2 Рис. 2.3
Если известны координаты точек ![]() и
и ![]() , то координаты вектора вычисляются по формулам:
, то координаты вектора вычисляются по формулам:
Формулы для вычисления длины вектора а, а также расстояния между точками и :
![]() . (2.2а)
. (2.2а)
Декартовы координаты вектора на плоскости определяются аналогично, с той разницей, что там отсутствует ось аппликат и, соответственно, третья координата. Таким образом, если а = и , то, очевидно,
![]() (2.2б)
(2.2б)
Определение 2.11. Обозначим a, b и g – углы наклона вектора а к координатным осям Ох , Оу и Оz , соответственно. Три числа cosa, cosb и cosg называются направляющими косинусами вектора а .
Справедливы равенства:
Формулы для вычисления направляющих косинусов:
Если равенства (2.4) возвести в квадрат и сложить, то получим:
Таким образом, сумма квадратов направляющих косинусов любого вектора равна единице .
Так как любой вектор однозначно определяется заданием трех его координат, то теперь мы видим, что любой вектор также однозначно определяется заданием его длины и направляющих косинусов.
Линейными операциями принято называть операцию сложения векторов и операцию умножения вектора на число.
Определение 2.12. Суммойа + b двух векторов а и b называется вектор, который идет из начала вектора а в конец вектора b , при условии, что вектор b приложен к концу вектора а .
 Существует два способа сложения векторов: по правилу треугольника (рис. 2.4) и по правилу параллелограмма (рис. 2.5).
Существует два способа сложения векторов: по правилу треугольника (рис. 2.4) и по правилу параллелограмма (рис. 2.5).
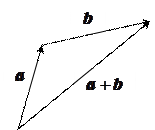
Рис. 2.4 Рис. 2.5
Сложение векторов обладает следующими свойствами:
1) переместительное свойство: а + b = b + a ;
2) сочетательное свойство: (a + b ) + c = a + (b + c ).
Определение 2.13. Вектор –а называется обратным вектору а , если он коллинеарен а , имеет длину, равную |a |, и направлен в противоположную сторону.
Очевидно, а + (–а ) = 0.
Определение 2.14. Разностью двух векторов a и b называется вектор a – b = a + (–b ).
На рис. 2.6 показано, как построить разность векторов двумя различными способами.
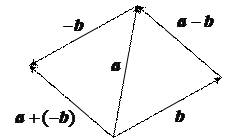
Определение 2.15. Произведением числа a на вектор а называется вектор aа , коллинеарный вектору а , имеющий длину |a|×|a | и направленный так же, как а , если a > 0, и в противоположную сторону, если a < 0. Если a = 0, то aа = 0.
Перечислим свойства, которыми обладает операция произведения вектора на число.
1. Распределительное свойство относительно суммы векторов: a(а + b ) = aa + ab .
2. Распределительное свойство относительно суммы чисел: (a + b)а = aа + bа .
3. Сочетательное свойство: a(bа ) = (ab)а .
4. Если вектор b коллинеарен вектору а , то существует число l такое, что b = la .
Вектор в декартовой системе координат
Определение. Вектором называется упорядоченная пара точек (начало вектора и его конец). Если , , то вектор имеет координаты .
Вектор в координатном пространстве Oxyz, может быть представлен в виде
Где тройка называется координатами вектора. Векторы - единичные векторы (орты), направленные в положительную сторону координатных осей Ox, Oy и Oz, соответственно. Длиной (модулем) вектора называется число .
Линейные операции с векторами
Сложение векторов определяется по правилу параллелограмма: вектор является диагональю параллелограмма, построенного на векторах и (рис.1а).
Разность двух векторов и определяется по формуле , где - вектор той же длины, что и вектор , но противоположно направленный. Чтобы найти вектор-разность нужно отложить векторы и из общей точки, соединить концы векторов вектором, направленным от «вычитаемого» к «уменьшаемому» (то есть от к ) (рис.1б). Построенный вектор и будет искомой разностью.
При сложении нескольких векторов каждая координата суммы есть сумма соответствующих координат слагаемых векторов, при умножении вектора на данное число на это же число умножаются и координаты вектора:
б) , где - скалярный множитель.
Несколько векторов называются коллинеарными (компланарными), если они параллельны одной и той же прямой (плоскости). Векторы и параллельны (коллинеарны), то есть соответствующие координаты этих векторов пропорциональны с одним и тем же коэффициентом пропорциональности: .
Базис на плоскости и в пространстве
Определение. Базисом на плоскости (в пространстве) называется упорядоченная пара (тройка) неколлинеарных (некомпланарных) векторов. Любой вектор однозначным образом раскладывается по базису. Коэффициенты разложения называются координатами этого вектора относительно данного базиса. Векторы образуют базис в декартовом координатном пространстве Oxyz.
Даны векторы . Показать, что векторы и образуют базис на плоскости и найти координаты вектора в этом базисе.
Решение. Если два вектора неколлинеарны (), то они образуют базис на плоскости. Так как , то векторы и неколлинеарны и, значит, образуют базис. Пусть в этом базисе вектор имеет координаты , тогда разложение вектора по векторам и имеет вид , или в координатной форме
Решив полученную систему уравнений каким-либо образом, получим, что.
Значит . Таким образом, в базисе вектор имеет координаты .
Скалярное, векторное, смешанное произведение векторов.
Определение. Скалярным произведением двух векторов и называется число, определяемое равенством:
где - угол между векторами и . Если , то .
Зная скалярное произведение, можно определить угол между двумя векторами по формуле: .
Условие перпендикулярности ненулевых векторов (угол между ними равен 90°) имеет вид: , или , а условие их коллинеарности: , или .
Свойства скалярного произведения:
1) ; 2) ; 3) ; 4) , причем .
Пример 2. Найти угол между векторами и , если , , , .
Решение. Используем формулу . Определим координаты векторов и , учитывая, что при сложении векторов мы складываем одноименные координаты, а при умножении вектора на число - умножаем на это число каждую координату этого вектора, а: , .
Найдем скалярное произведение векторов и и их длины. , , . Подставив в формулу, получим . Отсюда .
Определение. Векторным произведением вектора на вектор называется вектор (другое обозначение ), который:
а) имеет длину , где - угол между векторами и ;
б) перпендикулярен векторам и () (то есть, перпендикулярен плоскости, в которой лежат векторы и );
в) направлен так, что векторы , , образуют правую тройку векторов, то есть из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки (рис.2).
Координаты векторного произведения вектора на вектор определяются по формуле:
Геометрический смысл векторного произведения: модуль вектора равен площади параллелограмма, построенного на векторах и .
Свойства векторного произведения:
3) ; 4) и коллинеарны.
Пример 3. Параллелограмм построен на векторах и , где , , . Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
Угол между диагоналями обозначим буквой , тогда
Следовательно, .
Используя свойства векторного произведения, вычислим площадь параллелограмма:
Определение. Смешанным произведением трех векторов , , называется скалярное произведение вектора на вектор :
Если то смешанное произведение можно вычислить по формуле:
Свойства смешанного произведения:
1) При перестановке любых двух векторов смешанное произведение меняет знак;
4) компланарны .
Геометрический смысл смешанного произведения: объем параллелепипеда, построенного на векторах , , (рис.4), а объем образованной ими треугольной пирамиды находятся по формулам .
Пример 4. Компланарны ли векторы , , ?
Решение. Если векторы компланарны, то по свойству 4) их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов, вычислив определитель:
векторы , , некомпланарны.
Деление отрезка в данном отношении.
Пусть отрезок в пространстве Oxyz задан точками и . Если он разделен точкой в отношении , то координаты точки следующие:
Пример 5. Найти точку , делящую отрезок в отношении , если .
Решение. Определим координаты точки :
Таким образом, .
Аналитическая геометрия.
Уравнение плоскости. Общее уравнение плоскости имеет вид: , , где - нормальный вектор плоскости (т.е. перпендикулярный плоскости), а коэффициент пропорционален расстоянию от начала координат до плоскости.
Уравнение плоскости, проходящей через точку перпендикулярно вектору , имеет вид
Уравнение плоскости, проходящей через три заданные точки , и имеет вид:
Угол между двумя плоскостями, имеющими нормальные векторы и , определяется как угол между векторами и по формуле:
Расстояние от точки до плоскости вычисляется по формуле .
Пример 6. Написать уравнение плоскости, проходящей через точки , , .
Решение. Воспользуемся уравнением плоскости, проходящей через три заданные точки. Вычислим определитель
Или - искомое уравнение плоскости.
Уравнение прямой на плоскости. Общее уравнение прямой на плоскости имеет вид: , где - нормальный вектор прямой (перпендикулярный прямой), а коэффициент пропорционален расстоянию от начала координат до прямой.
Уравнение прямой, проходящей через данную точку , имеет вид
В другом виде , где - тангенс угла, образованного прямой и положительным направлением оси Ox, называемый угловым коэффициентом, b - ордината точки пересечения прямой с осью Oy.
Уравнение прямой, проходящей через две заданные точки и , имеет вид
Угол между двумя прямыми и определяется формулой
Расстояние от точки до прямой находится по формуле
Пример 7. Даны уравнения двух сторон прямоугольника , и уравнение его диагонали . Составить уравнения
остальных сторон и второй диагонали этого прямоугольника.
Решение. Сделаем схематический чертеж (Рис.6). Перепишем данные уравнения в виде: , , . Так как угловые коэффициенты прямых, задающих стороны прямоугольника, одинаковы , то эти уравнения задают параллельные прямые, то есть стороны, на них лежащие, противоположны. Найдем точки пересечения данной диагонали с этими сторонами. Пусть это будут точки и . Для этого приравняем сначала 1 и 3, а затем 2 и 3 уравнения:
; . Таким образом, .
Неизвестные стороны параллельны между собой и перпендикулярны данным (так как это прямоугольник).
Замечание. Угловые коэффициенты перпендикулярных прямых и связаны соотношением .
Таким образом, уравнения неизвестных сторон прямоугольника таковы:
Подставив в первое уравнение координаты точки , во второе - точки , получим, что и, следовательно, , .
Найдем координаты точек и , приравняв уравнения соответствующих сторон:
То есть ;
То есть .
Уравнение диагонали получим как уравнение прямой, проходящей через две заданные точки и :
Уравнения прямой в пространстве. Прямая в пространстве Oxyz определяется как линия пересечения двух плоскостей (общие уравнения прямой в пространстве).
Канонические уравнения прямой в пространстве имеют вид
где - точка, через которую проходит прямая, а вектор , параллельный данной прямой, называется направляющим вектором прямой.
Уравнения прямой в пространстве, проходящей через две заданные точки и имеют вид
Угол между двумя прямыми с направляющими векторами и определяется по формуле
Пример 8. Пирамида задана координатами своих вершин , , . Требуется найти:
1) длины ребер и ; 2) угол между ребрами и ; 3) площадь грани, содержащей вершины ; 4) объем пирамиды; 5) уравнения прямых и ;
6) уравнение высоты , опущенной из вершины на плоскость ;
7) расстояние от вершины до плоскости ; 8) угол между ребром и гранью, содержащей вершины .
Решение.1) Длины ребер и определим как модуль векторов и по формулам ;
2) Найдем координаты векторов и :
Длины этих векторов, т.е. длины ребер и , таковы: ,
Косинус угла между ребрами и вычислим по формуле ;
3) Площадь грани (треугольника) равна половине площади параллелограмма, построенного на векторах и , т.е. половина модуля векторного произведения этих векторов, которое равно
Тогда, (кв. ед);
4) Объем пирамиды равен .
5) Уравнения прямых и найдем как уравнения прямых, проходящих через две данные точки:
(): (абсциссы точек и одинаковые);
6) Направляющим вектором высоты является нормальный вектор плоскости . Получим уравнение плоскости :
Уравнение плоскости . Тогда нормальный вектор плоскости имеет координаты . Канонические уравнения прямой, проходящей через точку параллельно вектору имеет вид: ;
7) Для вычисления расстояния от вершины до плоскости воспользуемся формулой . В нашем случае - уравнение плоскости и . Итак, ;
8) Угол между прямой и плоскостью находят по формуле:
Где - нормальный вектор плоскости . и (см. п.7) . Таким образом, ,
Кривые второго порядка
Определение. Параболой называется множество точек плоскости (см. рис.7а), для каждой из которых расстояние до данной точки (фокуса параболы) равно расстоянию до некоторой данной прямой (директрисы). Расстояние от фокуса параболы до директрисы называется параметром параболы. Парабола - симметричная кривая; точка пересечения параболы с ее осью симметрии называется вершиной параболы.
Каноническое уравнение параболы в декартовой системе координат: .
Определение. Эллипс есть множество точек плоскости (см. рис.7б), для каждой из которых сумма расстояний до двух данных точек и (фокусов) постоянна и равна .
Отрезок называется фокусным расстоянием и обозначается через . Середина есть центр эллипса. Прямая, на которой лежат фокусы эллипса, называется первой осью эллипса. Прямая, проходящая через центр эллипса перпендикулярно его первой оси, называется второй осью эллипса. Оси эллипса являются его осями симметрии. Точки пересечения эллипса с осями симметрии называются его вершинами. - большая ось эллипса, - малая ось.
Директрисой эллипса, соответствующей данному фокусу , называется прямая , перпендикулярная первой оси и отстоящая от центра эллипса на расстояние , где - эксцентриситет эллипса.
Каноническое уравнение эллипса в декартовой системе координат: , где и - большая и малая полуоси эллипса, соответственно.
Определение. Гиперболой называется множество точек плоскости (см. рис.8) , модуль разности расстояний которых до двух данных точек и (фокусов гиперболы) постоянен и равен . Фокусное расстояние обозначают через . Прямая, на которой лежат фокусы, называется действительной (или фокальной осью) гиперболы. Прямая, проходящая через центр гиперболы , перпендикулярно к действительной оси, называется
мнимой осью.
Директрисой гиперболы, соответствующей данному фокусу , называется прямая , перпендикулярная к действительной оси, отстоящая от центра на расстояние и лежащая от центра по одну сторону с фокусом, где - эксцентриситет.
Гипербола имеет две асимптоты, заданные уравнениями .
Каноническое уравнение гиперболы в декартовой системе координат: ,
где и - половины сторон основного прямоугольника гиперболы.
Пример 9. Определить вид линии второго порядка, заданной уравнением
Решение. Выделим полные квадраты по х и по у, получим:
т.е. имеем гиперболу, центр которой лежит в точке , .
Полярные координаты. Для точки в плоскости Oxy ее полярные координаты определяются парой чисел , где - длина вектора , а - угол наклона вектора к полярной оси (положительного направления оси Ox), - длина вектора .
Декартовые и полярные координаты связаны следующими соотношениями.